题目内容
 如图所示,在场强大小E=
如图所示,在场强大小E=| 3 |
分析:以小物块为研究对象,分析受力情况,根据牛顿第二定律求出加速度.物块沿斜面向下做匀加速运动,由速度位移公式求解物块滑到斜面底端的速度大小.
解答:解:以小物块为研究对象,分析受力情况:重力mg、电场力F和斜面的支持力N.其中 电场力F=QE=2×10-8C×
电场力F=QE=2×10-8C×
×108N/C=2
N
根据牛顿第二定律得
加速度a=
代入解得a=8m/s2
物块下滑距离为S=
=2H=1m
由v2=2aS得
得v=
=
m/s=4m/s
答:物块滑到斜面底端的速度大小为4m/s.
 电场力F=QE=2×10-8C×
电场力F=QE=2×10-8C×| 3 |
| 3 |
根据牛顿第二定律得
加速度a=
| mgsin30°+Fcos30° |
| m |
代入解得a=8m/s2
物块下滑距离为S=
| H |
| sin30° |
由v2=2aS得
得v=
| 2aS |
| 2×8×1 |
答:物块滑到斜面底端的速度大小为4m/s.
点评:本题也可以根据动能定理这样列式求解:(mgsin30°+Fcos30°)S=
mv2.基础题.
| 1 |
| 2 |

练习册系列答案
相关题目
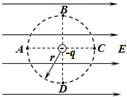 如图所示,在场强大小为E,方向水平向右的匀强电场中,放一个电荷量为-q的点电荷,A、B、C、D四点在以点电荷为圆心、半径为r的圆周上,并且A点、C点与点电荷在同一水平线上,B点、D点与点电荷在同一竖直线上,则下列说法正确的是( )
如图所示,在场强大小为E,方向水平向右的匀强电场中,放一个电荷量为-q的点电荷,A、B、C、D四点在以点电荷为圆心、半径为r的圆周上,并且A点、C点与点电荷在同一水平线上,B点、D点与点电荷在同一竖直线上,则下列说法正确的是( )A、A点电场强度最大,且为E+k
| ||
| B、B、D两点电场强度大小相等,方向相同 | ||
| C、同一点电荷在B点和D点时的电势能相等 | ||
| D、同一点电荷在A点和C点时的电势能相等 |
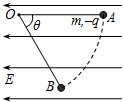 (2006?淮安二模)如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )
(2006?淮安二模)如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( ) 如图所示,在场强大小为E的水平匀强电场中,一根不可伸长的长度为L的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平面成θ=60°的位置B时速度为零,以下说法正确的是( )
如图所示,在场强大小为E的水平匀强电场中,一根不可伸长的长度为L的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平面成θ=60°的位置B时速度为零,以下说法正确的是( )