题目内容
2.杂技演员表演“水流星”,使装有水的瓶子在竖直平面内做半径为0.9m的圆周运动,若瓶内盛有100g的水,平的质量为400g,当瓶运动到最高点时,瓶口向下,要使水不流出来,瓶子的速度至少为3m/s;绳子收到的拉力为0N,若在最低点的速度是临界速度的2倍,则此时,绳子收到的拉力为25 N.(g=10m/s)分析 在最高点,临界状态时,拉力为零,靠重力提供向心力,根据牛顿第二定律求出瓶子的速度,根据向心力的公式求出向心力的大小.临界情况下绳子的拉力为零.
在最低点,根据向心力公式求出水的向心力大小,对整体分析,根据牛顿第二定律求出绳子的拉力.对水分析,根据牛顿第二定律求出桶底对水的作用力
解答 解:瓶子运动至最高点时,
由mg+F=m$\frac{{V}^{2}}{R}$得,当F拉=0时,v=$\sqrt{gR}$=3 m/s
对水而言:F向=m水$\frac{{V}^{2}}{R}$=1 N
此时绳子的拉力为0.
在最低点时:由F-mg=m$\frac{{V}^{2}}{R}$
对水而言:F向=m水$\frac{{V}^{2}}{R}$=4 N
对瓶和水整体而言:F′向=(m水+m瓶)$\frac{{V}^{2}}{R}$=20 N
而F向=F拉-(m+M)g
得F拉=F′向+(m+M)g=20+5=25 N
故答案为:3;0;25
点评 解决本题的关键掌握物体做圆周运动向心力的来源,抓住临界情况,通过牛顿第二定律进行求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 如图,一固定斜面上两个质量均为m的小物块A和B紧挨着匀速F滑,A与B的接触面光滑A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为a,则木块A、B之间的弹力为多少( )
如图,一固定斜面上两个质量均为m的小物块A和B紧挨着匀速F滑,A与B的接触面光滑A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为a,则木块A、B之间的弹力为多少( )
 如图,一固定斜面上两个质量均为m的小物块A和B紧挨着匀速F滑,A与B的接触面光滑A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为a,则木块A、B之间的弹力为多少( )
如图,一固定斜面上两个质量均为m的小物块A和B紧挨着匀速F滑,A与B的接触面光滑A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为a,则木块A、B之间的弹力为多少( )| A. | $\frac{1}{3}$mgsinθ | B. | $\frac{2}{3}$mgsinθ | C. | $\frac{4}{3}$mgsinθ | D. | mgsinθ |
10.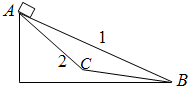 物块先沿轨道1从A点由静止下滑至底端B点,后沿轨道2从A点由静止下滑经C点至底端C点,AC=CB,如图所示.物块与两轨道的动摩擦因数相同,不考虑物块在C点处撞击的因素,则在物块整个下滑过程中( )
物块先沿轨道1从A点由静止下滑至底端B点,后沿轨道2从A点由静止下滑经C点至底端C点,AC=CB,如图所示.物块与两轨道的动摩擦因数相同,不考虑物块在C点处撞击的因素,则在物块整个下滑过程中( )
 物块先沿轨道1从A点由静止下滑至底端B点,后沿轨道2从A点由静止下滑经C点至底端C点,AC=CB,如图所示.物块与两轨道的动摩擦因数相同,不考虑物块在C点处撞击的因素,则在物块整个下滑过程中( )
物块先沿轨道1从A点由静止下滑至底端B点,后沿轨道2从A点由静止下滑经C点至底端C点,AC=CB,如图所示.物块与两轨道的动摩擦因数相同,不考虑物块在C点处撞击的因素,则在物块整个下滑过程中( )| A. | 物块到达B端时的动能不同 | B. | 物块沿两条轨道下滑的位移相同 | ||
| C. | 物块滑至B点时速度相同 | D. | 两种情况下损失的机械能相同 |
17.关于功和能,下列说法正确的是( )
| A. | 通过做功可以使不同形式的能量之间发生相互转化,但能量的总量是守恒的 | |
| B. | 功和能的单位相同,他们的概念也相同 | |
| C. | 做功的过程一定是物体的能量增加的过程 | |
| D. | 做功的过程一定是物体的能量减少的过程 |
7.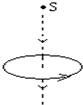 1931年,英国物理学家狄拉克从理论上预言存在着只有一个磁极的粒子--磁单极子,当磁单极子(S极)从上至下穿过一闭合导体环,以下说法正确的有( )
1931年,英国物理学家狄拉克从理论上预言存在着只有一个磁极的粒子--磁单极子,当磁单极子(S极)从上至下穿过一闭合导体环,以下说法正确的有( )
 1931年,英国物理学家狄拉克从理论上预言存在着只有一个磁极的粒子--磁单极子,当磁单极子(S极)从上至下穿过一闭合导体环,以下说法正确的有( )
1931年,英国物理学家狄拉克从理论上预言存在着只有一个磁极的粒子--磁单极子,当磁单极子(S极)从上至下穿过一闭合导体环,以下说法正确的有( )| A. | 进入环时,环中感应电流方向和图所示方向相同 | |
| B. | 进入环时,环中感应电流方向和图所示方向相反 | |
| C. | 离开环时,环中感应电流方向和图所示方向相反 | |
| D. | 离开环时,环中感应电流方向和图所示方向相同 |
12.设斜上抛物体在通过轨迹的最高位置时,突然炸裂成质量不等的两块,已知其中一块沿原水平方向做平抛运动,则另一块的运动可能是( )
| A. | 反方向平抛运动 | B. | 斜上抛运动 | C. | 自由落体运动 | D. | 原方向平抛运动 |

 如图所示的电场中,将3C的正电荷分别由A、C两点移动都B点,静电力做的功分别是36J、-12J.如果取B点为零电势点,A、C两点的电势分别是φA=12V,φC=-4V,A、C间的电势差UAC=16V;如果取A为零电势点,那么φB=-12V,φC=-16V,UAC=16V.
如图所示的电场中,将3C的正电荷分别由A、C两点移动都B点,静电力做的功分别是36J、-12J.如果取B点为零电势点,A、C两点的电势分别是φA=12V,φC=-4V,A、C间的电势差UAC=16V;如果取A为零电势点,那么φB=-12V,φC=-16V,UAC=16V.