题目内容
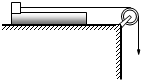 如图所示,一质量为m1、长为L的长木板放在很长的光滑水平桌面上,板的左端有一质量为m2的小滑块.滑块用一很长细线跨过桌面边沿定滑轮,现以恒定速度v向下拉线,滑块最多只能到达板的中点,已知整个过程板的右端都不会到达桌面边沿.试求
如图所示,一质量为m1、长为L的长木板放在很长的光滑水平桌面上,板的左端有一质量为m2的小滑块.滑块用一很长细线跨过桌面边沿定滑轮,现以恒定速度v向下拉线,滑块最多只能到达板的中点,已知整个过程板的右端都不会到达桌面边沿.试求(1)当滑块刚到达木板中点时木板的位移;
(2)若木板与桌面间有摩擦,为使滑块能达到木板的右端,木板与桌面间的动摩擦因数应满足什么条件?
分析:(1)由题意知,滑块做匀速运动,木板做匀加速运动,当滑块滑到木板的中点时,两者速度相等,均为v,运用运动学公式分别表示两个物体的位移,根据位移之差等于
L,即可求出木板的位移;
(2)当桌面光滑时,由牛顿第二定律和运动学结合求出滑块与长木板之间摩擦因数μ1.如果板与桌面有摩擦,因为长木板与桌面摩擦因数越大,滑块越易从右端滑下,所以当滑块滑到长木板右端两者刚好共速时摩擦因数最小,设为μ2.对木板,运用牛顿第二定律和运动学公式列式,结合滑块与长木板的位移之差等于L,即可求得μ2.从而得到其范围.
| 1 |
| 2 |
(2)当桌面光滑时,由牛顿第二定律和运动学结合求出滑块与长木板之间摩擦因数μ1.如果板与桌面有摩擦,因为长木板与桌面摩擦因数越大,滑块越易从右端滑下,所以当滑块滑到长木板右端两者刚好共速时摩擦因数最小,设为μ2.对木板,运用牛顿第二定律和运动学公式列式,结合滑块与长木板的位移之差等于L,即可求得μ2.从而得到其范围.
解答:解:(1)滑块与长木板相对滑动过程
小滑块m1匀速运动,则有:vt=s1 ①
长木板m2匀加速运动,则有:
vt=s2 ②
又几何关系得:s1-s2=
L ③
联立以上三式得s2=
L
(2)设滑块与长木板之间摩擦因数为μ1
当桌面光滑时有 μ1m2g=m1a1 ④
v2=2a1s2 ⑤
由④⑤得μ1=
如果板与桌面有摩擦,因为长木板与桌面摩擦因数越大,滑块越易从右端滑下,所以当滑块滑到长木板右端两者刚好共速时摩擦因数最小,设为μ2
对长木板有:m1a2=μ1m2g-μ2(m1+m2)g ⑥
t′=s′2 ⑦
v2=2a2s′2 ⑧
对滑块有:vt′=s′1 ⑨
又 s′1-s′2=L ⑩
联立以上五式得 μ2=
所以桌面与板间的摩擦因数μ≥
答:
(1)当滑块刚到达木板中点时木板的位移是
L;
(2)若木板与桌面间有摩擦,为使滑块能达到木板的右端,木板与桌面间的动摩擦因数应满足的条件是μ≥
.
小滑块m1匀速运动,则有:vt=s1 ①
长木板m2匀加速运动,则有:
| 1 |
| 2 |
又几何关系得:s1-s2=
| 1 |
| 2 |
联立以上三式得s2=
| 1 |
| 2 |
(2)设滑块与长木板之间摩擦因数为μ1
当桌面光滑时有 μ1m2g=m1a1 ④
v2=2a1s2 ⑤
由④⑤得μ1=
| m1v2 |
| m2gL |
如果板与桌面有摩擦,因为长木板与桌面摩擦因数越大,滑块越易从右端滑下,所以当滑块滑到长木板右端两者刚好共速时摩擦因数最小,设为μ2
对长木板有:m1a2=μ1m2g-μ2(m1+m2)g ⑥
| v |
| 2 |
v2=2a2s′2 ⑧
对滑块有:vt′=s′1 ⑨
又 s′1-s′2=L ⑩
联立以上五式得 μ2=
| m1v2 |
| 2(m1+m2)gL |
所以桌面与板间的摩擦因数μ≥
| m1v2 |
| 2(m1+m2)gL |
答:
(1)当滑块刚到达木板中点时木板的位移是
| 1 |
| 2 |
(2)若木板与桌面间有摩擦,为使滑块能达到木板的右端,木板与桌面间的动摩擦因数应满足的条件是μ≥
| m1v2 |
| 2(m1+m2)gL |
点评:明确临界条件,弄清物块和木板之间的位移、速度、加速度关系是解答本题的关键.

练习册系列答案
相关题目
 如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为
如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为 如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2
如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2 如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( )
如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( ) 如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( )
如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( ) 如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.
如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.