题目内容
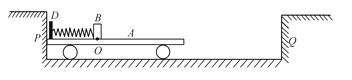
【题目】如图所示，在光滑水平面左、右两侧各有一竖直弹性墙壁P、Q，平板小车A的左侧固定一挡板D，小车和挡板的总质量M＝2 kg，小车上表面O点左侧光滑，右侧粗糙，一轻弹簧左端与挡板相连，原长时右端在O点．质量m＝1 kg的物块B在O点贴着弹簧右端放置，但不与弹簧连接，B与O点右侧平面间的动摩擦因数μ＝0.5.现将小车贴着P固定，用水平恒力F推B向左移动x0＝0.1 m距离时撤去推力，B继续向左运动，最终停在O点右侧x1＝0.9 m处，取重力加速度g＝10 m/s2，弹簧始终在弹性限度内．
(1) 求水平恒力F的大小及弹簧的最大弹性势能Ep；
(2) 撤去小车A的固定限制，以同样的力F推B向左移动x0时撤去推力，发现A与Q发生第一次碰撞前A、B已经达到共同速度，求最初A右端与Q间的最小距离s0；
(3) 在(2)的情况下，求B在O点右侧运动的总路程s及运动过程中B离开O点的最远距离x(车与墙壁碰撞后立即以原速率弹回)．
【答案】(1) 4.5 J(2) 0.2 m(3) 0.87 m
【解析】试题分析：（1）小车贴着P固定，对全过程研究，根据动能定理列式，可求出F．再由功能关系求弹簧的最大弹性势能
；（2）撤去小车A的固定限制，B离开弹簧后，B做减速运动，A做加速运动，根据牛顿第二定律求出两者的加速度，根据速度相等的条件列式，求出时间，再由位移公式求解最小距离
；（3）最终A、B都停止运动，机械能转化为内能，由功能关系求B在O点右侧运动的总路程s．根据速度关系，由速度公式求出时间，再求解运动过程中B离开O点的最远距离x．
（1）取全过程研究，根据动能定理
，解得
由功能关系
解得
（2）设B运动到O点的速度为
，根据机械能守恒定律得
接着B减速，设加速度大小为
，根据牛顿第二定律
A加速，设加速度大小为a2，根据牛顿第二定律
设运动的共同速度为v1，则
时间内A运动的距离即为最小距离
解得
（3）最终A、B都停止运动，机械能转化为内能，由功能关系得
解得
A与Q第一次碰撞前，B距离O点
解得
， 
这段时间内B相对A向右移动
此时B离开O点的最远距离
解得
