题目内容
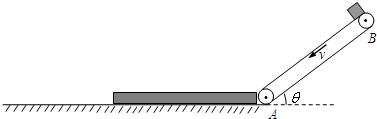
7.如图所示,与水平方向成θ=37°的传送带以恒定速度v=4m/s沿逆时针方向转动,两传动轮间距为lAB=5.8m.一质量为M=1kg的长木板静止在粗糙地面上,其右端靠着传送带.现将一质量为m=1kg且可视为质点的物块轻放在传送带顶端B点,物块沿传送带滑至底端,正好滑上长木板(此过程无机械能损失).已知物块与传送带间的动摩擦因数为μ1=0.5,物块与长木板间的动摩擦因数为μ2=0.4,长木板与地面间的动摩擦因素为μ3=0.1,重力加速度g=10m/s2;求:A.物块刚滑到长木板上的速度大小;
B.从滑块滑上长木板到二者停下的总时间;
C.为保证滑块不从长木板上滑下,长木板的最小长度.
分析 A、根据牛顿第二定律可求得物体的加速度,再由运动学公式可求得物块刚滑到长木板上时的速度大小;
B、分别对滑块和木板进行分析,根据牛顿第二定律求出各自的加速度;再由运动学公式明确达共同速度的时间;再对整体分析,由牛顿第二定律及运动学公式可求得停止的时间;
C、根据运动学公式求得两小球达到共速时所经历的位移,再由位移公式求解各自的位移,即可明确最小长度.
解答 解:A、物体轻放上传送带,根据牛顿第二定律可得:
mgsinθ+μ1mgcosθ=ma1
解得:a1=10m/s2;
物体以a1速至v2:
则有:v2=2a1l1
解得:l1=0.8m;
到达v之后以a2加速到B:
mgsinθ-μ1mgcosθ=ma2
解得:a2=2m/s2;
到达B速度为v0:
v20-v2=2a2(lAB-l1)
解得:v0=6m/s
B、滑块滑上长木板,对滑块有:
μ2mg=ma3
解得:a3=4m/s2;
方向向右;
对长木板:μ2mg-μ3(m+M)g=ma4
解得:a4=2m/s2;
方向向左;
二者速度相等经历的时间为t1:
则由速度公式可得:v0-a3t1=a4t1
解得:t1=1s;
速度为v1=2m/s;
共速后再共同匀减速,μ3(M+m)g=(M+m)a5
解得:a5=1m/s2
再到停下:t2=$\frac{{v}_{1}}{{a}_{5}}$=$\frac{2}{1}$=2s;
故总时间t=t1+t2=1+2=3s;
C、达到共同速度时,滑块的位移x1=v0t1-$\frac{1}{2}$a3t12=6×1-$\frac{1}{2}$×2×12=5m;
木板的位移x2=$\frac{1}{2}$a4t12=$\frac{1}{2}$×2×12═1m;
故木板的长度至少为:x1-x2=5-1=4m;
答:A、物块刚滑到长木板上的速度大小为6m/s;
B、从滑块滑上长木板到二者停下的总时间为3s;
C、为保证滑块不从长木板上滑下,长木板的最小长度4m.
点评 本题考查牛顿第二定律的应用,涉及两个物体多个过程,要注意正确确定研究对象,做好受力分析,再根据牛顿第二定律结合运动学公式进行分析求解;注意掌握应用加速度的桥梁作用.

 习题精选系列答案
习题精选系列答案| A. | 中央电视台新闻联播节目用时30分钟 | |
| B. | 1997年7月1日零时中国对香港恢复行使主权 | |
| C. | 2007年10月24日18时5分5秒嫦娥一号在西昌卫星发射中心升空 | |
| D. | 北京奥运会开幕式于2008年8月8日晚8时开始 |
| A. |  真空冶炼炉是利用涡流来熔化金属的装置 | |
| B. |  家用电磁炉锅体中的涡流是由恒定磁场产生的 | |
| C. |  阻尼摆摆动时产生的涡流总是阻碍其运动 | |
| D. |  变压器的铁芯用相互绝缘的硅钢片叠成能减小涡流 |
| A. | 当分子间的距离为r0时,分子力为零,也就是说分子间既无引力又无斥力 | |
| B. | 分子间距离大于r0时,分子间距离变小时,分子力一定减小 | |
| C. | 分子间距离小于r0时,分子间距离变小时,分子间斥力变大,引力变小 | |
| D. | 在分子力作用范围内,不管r>r0时,还是r<r0时,斥力总是比引力变化快 |
| A. | 能就是功,功就是能 | |
| B. | 物体做功越多,物体的能量就越大 | |
| C. | 外力对物体不做功,这个物体就没有能量 | |
| D. | 能量转化的多少可以用做功来量度 |
 某物理学习小组在探究超重、失重现象时设计了一款超、失重演示仪,其设计方法是用两根细铁丝作为一小铁球的运动轨道,两铁丝轨道之间的距离能保证小球恰好能停在A、B两点而不至于从轨道上漏下去(如图所示),然后让小球从O点滑下(O 点相对于A、B有足够的高度差),在小球沿轨道下滑的过程中( )
某物理学习小组在探究超重、失重现象时设计了一款超、失重演示仪,其设计方法是用两根细铁丝作为一小铁球的运动轨道,两铁丝轨道之间的距离能保证小球恰好能停在A、B两点而不至于从轨道上漏下去(如图所示),然后让小球从O点滑下(O 点相对于A、B有足够的高度差),在小球沿轨道下滑的过程中( )| A. | 小球能够从A点通过 | B. | 小球不能够从A点通过 | ||
| C. | 小球能够从B点通过 | D. | 小球不能够从B点通过 |
 如果把水星和金星绕太阳的运动视为匀速圆周运动,天文学家进行了这样的观测:如图所示,当太阳与水星、金星处在同一条直线上时开始计时,经过一段时间后,水星转过的角度为θ1;金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )
如果把水星和金星绕太阳的运动视为匀速圆周运动,天文学家进行了这样的观测:如图所示,当太阳与水星、金星处在同一条直线上时开始计时,经过一段时间后,水星转过的角度为θ1;金星转过的角度为θ2(θ1、θ2均为锐角),则由此条件可求得( )| A. | 水星和金星绕太阳运动的周期之比 | |
| B. | 水星和金星的密度之比 | |
| C. | 水星和金星做圆周运动的轨道半径之比 | |
| D. | 水星和金星绕太阳运动的向心加速度之比 |
 如图所示,一个内壁光滑的圆柱形汽缸,高度为L、底面积为S,缸内有一个质量为m的活塞,封闭了一定质量的理想气体.温度为热力学温标T0时,用绳子系住汽缸底,将汽缸倒过来悬挂起来,汽缸处于竖直状态,缸内气体高为L0.已知重力加速度为g,大气压强为p0,不计活塞厚度及活塞与缸体的摩擦,求:
如图所示,一个内壁光滑的圆柱形汽缸,高度为L、底面积为S,缸内有一个质量为m的活塞,封闭了一定质量的理想气体.温度为热力学温标T0时,用绳子系住汽缸底,将汽缸倒过来悬挂起来,汽缸处于竖直状态,缸内气体高为L0.已知重力加速度为g,大气压强为p0,不计活塞厚度及活塞与缸体的摩擦,求: