题目内容
一步行者以8m/s之速度在一直线道路上追赶一辆同向行驶而被红灯所阻之静止公车,当他距公车30米时,交通灯改变,公车以2m/s2加速度驶去,则人车之最短距离为 米.
【答案】分析:步行者做匀速运动,汽车从静止开始做匀加速运动,根据两者速度的关系分析两者之间距离的变化,可知当两者速度相等时,相距最近,根据速度公式求出时间,再由位移公式求解最短距离.
解答:解:步行者做匀速运动,汽车从静止开始做匀加速运动,开始时,步行者速度大于汽车的速度,两者距离减小;当汽车的速度大于步行者速度时,两者距离增大.故当两者速度相等时,距离最短,设速度相等时所用时间为t,则有
v人=at,得t=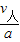 =
= s=4s
s=4s
则人车之最短距离为Smin=(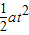 +30)-v人t=(
+30)-v人t=( +30)-8×4=14(m)
+30)-8×4=14(m)
故答案为:14.
点评:本题是追及问题,关键要寻找两车之间的关系,抓住隐含的临界条件:速度相等是关键.
解答:解:步行者做匀速运动,汽车从静止开始做匀加速运动,开始时,步行者速度大于汽车的速度,两者距离减小;当汽车的速度大于步行者速度时,两者距离增大.故当两者速度相等时,距离最短,设速度相等时所用时间为t,则有
v人=at,得t=
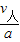 =
= s=4s
s=4s则人车之最短距离为Smin=(
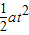 +30)-v人t=(
+30)-v人t=( +30)-8×4=14(m)
+30)-8×4=14(m)故答案为:14.
点评:本题是追及问题,关键要寻找两车之间的关系,抓住隐含的临界条件:速度相等是关键.

练习册系列答案
相关题目