题目内容
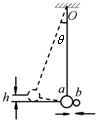 如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,偏角θ较小,摆动的周期为T,a球质量是b球质量的4倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后,摆动的周期为
如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,偏角θ较小,摆动的周期为T,a球质量是b球质量的4倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后,摆动的周期为分析:单摆的周期公式为T=π
,可见单摆的周期与摆球的质量无关.根据机械能守恒定律求出a球摆到最低点的速度,由动量守恒求出碰撞后共同体的速度,再由机械能守恒求解碰撞后摆球的最高点与最低点的高度差.
|
解答:解:根据单摆的周期公式为T=π
,单摆的周期与摆球的质量无关,则碰撞后,摆动的周期仍为T.
a球下摆过程,根据机械能守恒得 mgh=
mv2,得v=
碰撞过程,有 mv-
m?2v=
mv′,得v′=0.4v
碰撞后两球上摆过程,有
mgh′=
?
mv′2
联立解得,h′=0.16h
故答案为:1,0.16
|
a球下摆过程,根据机械能守恒得 mgh=
| 1 |
| 2 |
| 2gh |
碰撞过程,有 mv-
| 1 |
| 4 |
| 5 |
| 4 |
碰撞后两球上摆过程,有
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
联立解得,h′=0.16h
故答案为:1,0.16
点评:碰撞过程的基本规律是动量守恒定律,分析过程,确定规律是本题的解题关键.

练习册系列答案
相关题目
 (2007?北京)如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后( )
(2007?北京)如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后( ) (2012?黄埔区模拟)A、如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,偏角θ较小,摆动的周期为T,a球质量是b球质量的4倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后,摆动的周期为
(2012?黄埔区模拟)A、如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,偏角θ较小,摆动的周期为T,a球质量是b球质量的4倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后,摆动的周期为
 如图所示的单摆,摆球质量为m、摆长为l、重力加速度为g.现把摆球移到图中实线所示的位置,即摆线伸直且与竖直方向成一较小角度θ,从静止释放,求从开始运动到摆球第一次到达最低点过程中的①重力的冲量,②合外力的冲量.
如图所示的单摆,摆球质量为m、摆长为l、重力加速度为g.现把摆球移到图中实线所示的位置,即摆线伸直且与竖直方向成一较小角度θ,从静止释放,求从开始运动到摆球第一次到达最低点过程中的①重力的冲量,②合外力的冲量.