题目内容
【题目】如图所示,装置的中间是水平传送带,传送带始终以2m/s的速率逆时针转动,两边是光滑水平台面,传送带与左右两边的台面等高,并能平滑对接。左边台面的D点处放置着质量M=4kg的小物块A,O点距传送带左端L=1.2m。质量m=1kg的小物块B从右边台面上以v0=3m/s的初速度向左运动滑上传送带。已知物块B与传送带之间的动摩擦因数![]() =0.6,传送带水平部分的长度l=1.0m。设物块A、B间发生的是弹性碰撞,A与挡板碰撞中没有机械能损失,碰撞时间不计。两小物块均可视为质点,取g=10m/s2。
=0.6,传送带水平部分的长度l=1.0m。设物块A、B间发生的是弹性碰撞,A与挡板碰撞中没有机械能损失,碰撞时间不计。两小物块均可视为质点,取g=10m/s2。
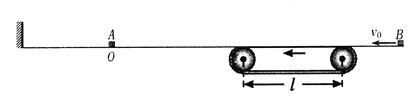
(1)求两物块第一次碰撞前物块B的速度大小v1,;
(2)若两物块发生第2次碰撞的位置仍在O处,求O与左侧挡板的距离;
(3)求第n次碰撞后,物块A的速度![]() 。
。
【答案】(1)2m/s(2)0.96m(3)当n为奇数时![]() ;当n为偶数时
;当n为偶数时![]()
【解析】(1)设B在传送带上一直做匀减速运动,到传送带左端时速度![]() ,根据牛顿第二定律和运动学公式可得
,根据牛顿第二定律和运动学公式可得![]() ①,
①,![]() ②
②
![]() 无解,即B不能一直减速,实际运动情况是减速到传送带速度相同后,做匀速运动,离开传送带后,与A第一次碰前,速度为
无解,即B不能一直减速,实际运动情况是减速到传送带速度相同后,做匀速运动,离开传送带后,与A第一次碰前,速度为![]() ③
③
(2)取向左为正方向,设A、B发生第一次碰撞后的速度分别为![]() 和
和![]() ,根据动量守恒定律和机械能守恒定律
,根据动量守恒定律和机械能守恒定律![]() ④,
④,![]() ⑤
⑤
由④⑤解得![]() ,
, ![]() ⑥
⑥
代入数据可得![]() ,
, ![]() ⑦
⑦
设O与左边挡板距离为x,到第二次碰撞经历的时间t。A在与挡板碰撞前后均做匀速运动![]() ⑧
⑧
B匀速到达传送带,在传送带上先减速到零,再反向加速,由于![]() 大小小于传送带的速度,所以离开传送带时,B的速度大小仍为
大小小于传送带的速度,所以离开传送带时,B的速度大小仍为![]() ,
, 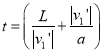 ⑨
⑨
代入数据可得x=0.96m
(3)取向左为正方向,第二次碰撞前,A向右运动![]() =-0.8m/s,B向左运动
=-0.8m/s,B向左运动![]()
设第二次碰撞后A的速度为![]() ,B的速度为
,B的速度为![]() ,根据动量守恒定律和机械能守恒定律
,根据动量守恒定律和机械能守恒定律
![]() ④,
④,![]()
联立代入数据可得![]() ,
, ![]()
即第二次碰撞后,A静止在O点,B以2m/s的速度向右冲上传送带,减速到零后向左加速,离开传送带时的速度为2m/s,重复第一次碰撞的过程,由(2)可知,第三次碰撞后AB的速度与第一次碰撞后的结果相同,一次类推,第四次碰撞后的结果与第二次
故当n为奇数时![]() ;当n为偶数时
;当n为偶数时![]()

 通城学典默写能手系列答案
通城学典默写能手系列答案