题目内容
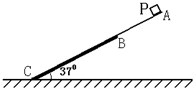
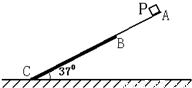
如图所示,倾斜角度为37的斜面,由AB和BC两部分组成.其中AB部分光滑,长为0.75m;BC部分粗糙,长为1.25m.物块(可看成质点)P从A点由静止释放,结果物块P在AB部分上做匀加速直线运动,加速度的大小为6m/s2;在BC部分上做匀减速直线运动,加速度大小为2m/s2,求:
(1)物块P运动至斜面C时的速度大小;
(2)物块P在斜面上运动的总时间.
【答案】分析:把整个运动过程分为两段,匀加速阶段与匀减速阶段,应用位移时间关系式与速度时间关系式分别解出末速度与总时间.
解答:解:(1)AB段做匀加速直线运动,
由位移时间关系式:xAB=
可得:tAB=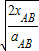 =0.5s
=0.5s
运动到B点速度:vB=aABtAB=3m/s
物体从B到C由位移时间关系式得:vC2-vB2=-2aBCxBC
解得:vC=2m/s
(2)BC段做匀减速直线运动,由速度时间关系式得:vC=vB-aBCtBC
解得:tBC=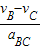 =0.5s
=0.5s
所以物块P在斜面上运动的总时间为:t=tAB+tBC=1.0s
答:(1)物块P运动至斜面C时的速度大小为2m/s;
(2)物块P在斜面上运动的总时间为0.5s.
点评:分析清楚物体运动的过程,先是匀加速直线运动,后是匀减速直线运动,分过程应用运动规律求解即可,本题的难度不大.
解答:解:(1)AB段做匀加速直线运动,
由位移时间关系式:xAB=

可得:tAB=
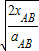 =0.5s
=0.5s运动到B点速度:vB=aABtAB=3m/s
物体从B到C由位移时间关系式得:vC2-vB2=-2aBCxBC
解得:vC=2m/s
(2)BC段做匀减速直线运动,由速度时间关系式得:vC=vB-aBCtBC
解得:tBC=
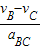 =0.5s
=0.5s所以物块P在斜面上运动的总时间为:t=tAB+tBC=1.0s
答:(1)物块P运动至斜面C时的速度大小为2m/s;
(2)物块P在斜面上运动的总时间为0.5s.
点评:分析清楚物体运动的过程,先是匀加速直线运动,后是匀减速直线运动,分过程应用运动规律求解即可,本题的难度不大.

练习册系列答案
相关题目
 如图所示,倾斜角度为θ的粗糙程度均匀的绝缘斜面,下方O点处有一带电量为+Q的点电荷,质量为m、带电量为-q的小物体(可看成质点)与斜面间的动摩擦因数为μ.现使小物体以初速度v0从斜面上的A点沿斜面上滑,到达B点时速度为零,然后又下滑回到A点.小物体所带电荷量保持不变,静电力常数为k,重力加速度为g,OA=OB=l.求:
如图所示,倾斜角度为θ的粗糙程度均匀的绝缘斜面,下方O点处有一带电量为+Q的点电荷,质量为m、带电量为-q的小物体(可看成质点)与斜面间的动摩擦因数为μ.现使小物体以初速度v0从斜面上的A点沿斜面上滑,到达B点时速度为零,然后又下滑回到A点.小物体所带电荷量保持不变,静电力常数为k,重力加速度为g,OA=OB=l.求: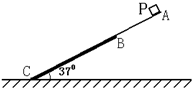 如图所示,倾斜角度为370的斜面,由AB和BC两部分组成.其中AB部分光滑,长为
如图所示,倾斜角度为370的斜面,由AB和BC两部分组成.其中AB部分光滑,长为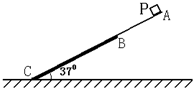 如图所示,倾斜角度为37°的斜面,由AB和BC两部分组成.其中光滑的AB部分长为0.75m;粗糙的BC部分长为1.5m.物块(可看成质点)P从A点由静止释放,结果物块P在AB部分上做匀加速直线运动,加速度的大小为6m/s2;在BC部分上做匀减速直线运动,到达C点时的速度恰好减为0.求:
如图所示,倾斜角度为37°的斜面,由AB和BC两部分组成.其中光滑的AB部分长为0.75m;粗糙的BC部分长为1.5m.物块(可看成质点)P从A点由静止释放,结果物块P在AB部分上做匀加速直线运动,加速度的大小为6m/s2;在BC部分上做匀减速直线运动,到达C点时的速度恰好减为0.求: