题目内容
 如图7所示,竖直平面内的
如图7所示,竖直平面内的| 3 | 4 |
(1)释放点距 A 点的竖直高度 h和落点 C 到 A 点的水平距离x;
(2)如果将小球由h=R处静止释放,请问小球能否通过最高点B点,如果不能通过,请求出脱离圆轨道的位置E与O的连线与竖直方向夹角的正弦值.
分析:(1)的关键是小球在B点时列出牛顿第二定律方程,再结合动能定理和平抛规律即可求解.
(2)的关键是先假设小球能到最高点,根据牛顿第二定律求出到达最高点的最小速度为
,与动能定理矛盾,说明不能到达最高点,然后设出E与O点连线的夹角,再根据动能定理和脱离轨道时牛顿第二定律即可求解.
(2)的关键是先假设小球能到最高点,根据牛顿第二定律求出到达最高点的最小速度为
| gR |
解答:解:(1)小球通过最高点B时,由牛顿第二定律,有:
mg+FN=m
又FN=mg
解得:vB=
设释放点到A点高度为h,小球从释放到运动至B点的过程中,
根据动能定理,有:mg(h-R)=
mvB2
解得:h=2R,
由平抛规律:R=
gt2
x=vBt,
联立解得x=2R,所以C点距A点距离:△x=2R-R=R
即释放点距A点的竖直高度h为2R,落点C到A点的水平距离为R.
(2)小球到达B点时最小速度为v,有:mg=m
若能到达最高点应满足mgR=
mv2+mgR,显然不可能成立,即不能到最高点.
设到最高点E的速度为vE,
E与O的连线与竖直方向夹角θ,由动能定理有:mgR(1-cosθ)=
mvE2…①,
在E点脱离轨道时有:mgcosθ=m
…②
联立①②解得:cosθ=
所以:sinθ=
答:(1)释放点距 A 点的竖直高度 h和落点 C 到 A 点的水平距离为R;
(2)如果将小球由h=R处静止释放,小球不能通过最高点B点,小球脱离圆轨道的位置E与O的连线与竖直方向夹角的正弦值为
.
mg+FN=m
| vB2 |
| R |
又FN=mg
解得:vB=
| 2gR |
设释放点到A点高度为h,小球从释放到运动至B点的过程中,
根据动能定理,有:mg(h-R)=
| 1 |
| 2 |
解得:h=2R,
由平抛规律:R=
| 1 |
| 2 |
x=vBt,
联立解得x=2R,所以C点距A点距离:△x=2R-R=R
即释放点距A点的竖直高度h为2R,落点C到A点的水平距离为R.
(2)小球到达B点时最小速度为v,有:mg=m
| v 2 |
| R |
若能到达最高点应满足mgR=
| 1 |
| 2 |
设到最高点E的速度为vE,
E与O的连线与竖直方向夹角θ,由动能定理有:mgR(1-cosθ)=
| 1 |
| 2 |
在E点脱离轨道时有:mgcosθ=m
| vE2 |
| R |
联立①②解得:cosθ=
| 2 |
| 3 |
所以:sinθ=
| ||
| 3 |
答:(1)释放点距 A 点的竖直高度 h和落点 C 到 A 点的水平距离为R;
(2)如果将小球由h=R处静止释放,小球不能通过最高点B点,小球脱离圆轨道的位置E与O的连线与竖直方向夹角的正弦值为
| ||
| 3 |
点评:小球在内侧轨道到达最高点时的最小速度应满足mg=m
,脱离轨道时应满足mgcosθ=m
,小球运动过程可利用动能定理或机械能守恒定律列式求解,小球平抛运动则利用平抛规律求解.
| v 2 |
| R |
| v 2 |
| R |

练习册系列答案
相关题目
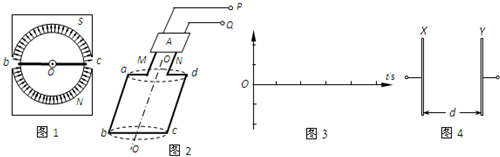 某种小发电机的内部结构平面图如图1所示,永久磁体的内侧为半圆柱面形状,它与共轴的圆柱形铁芯间的缝隙中存在辐向分布、大小近似均匀的磁场,磁感应强度B=0.5T.磁极间的缺口很小,可忽略.如图2所示,单匝矩形导线框abcd绕在铁芯上构成转子,ab=cd=0.4m,bc=0.2m.铁芯的轴线OO′在线框所在平面内,线框可随铁芯绕轴线转动.将线框的两个端点M、N接入图中装置A,在线框转动的过程中,装置A能使端点M始终与P相连,而端点N始终与Q相连.现使转子以ω=200π rad/s角速度匀速转动.在图1中看,转动方向是顺时针的,设线框经过图1位置时t=0.(取π=3)
某种小发电机的内部结构平面图如图1所示,永久磁体的内侧为半圆柱面形状,它与共轴的圆柱形铁芯间的缝隙中存在辐向分布、大小近似均匀的磁场,磁感应强度B=0.5T.磁极间的缺口很小,可忽略.如图2所示,单匝矩形导线框abcd绕在铁芯上构成转子,ab=cd=0.4m,bc=0.2m.铁芯的轴线OO′在线框所在平面内,线框可随铁芯绕轴线转动.将线框的两个端点M、N接入图中装置A,在线框转动的过程中,装置A能使端点M始终与P相连,而端点N始终与Q相连.现使转子以ω=200π rad/s角速度匀速转动.在图1中看,转动方向是顺时针的,设线框经过图1位置时t=0.(取π=3)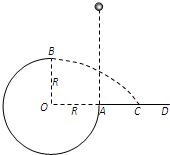
 圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求:
圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求: