题目内容
【题目】如图所示，一劲度系数为k的轻弹簧的上端固定，下端与小球相连接，小球的质量为m，小球静止于O点。现将小球拉到O点下方距离为A的位置，由静止释放，此后运动过程中始终未超过弹簧的弹性限度。规定平衡位置处为重力势能和弹簧弹性势能的零点。以平衡位置O为坐标原点建立如图所示的竖直向下的一维坐标系Ox．忽略空气阻力的影响。
（1）从运动与相互作用观点出发，解决以下问题：
a．求小球处于平衡状态时弹簧相对原长的伸长量s；
b．证明小球做简谐运动；
（2）从教科书中我们明白了由v﹣t图象求直线运动位移的思想和方法；从机械能的学习，我们理解了重力做功的特点并进而引入重力势能，由此可以得到重力做功与重力势能变化量之间的关系。图象法和比较法是研究物理问题的重要方法，请你借鉴此方法，从功与能量的观点出发，解决以下问题：
a．小球运动过程中，小球相对平衡位置的位移为x时，证明系统具有的重力势能
和弹性势能
的总和Ep的表达式为
；
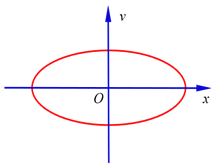
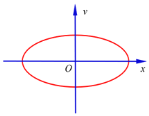
b．求小球在振动过程中，运动到平衡位置O点下方距离为
时的动能Ek．并根据小球运动过程中速度v与相对平衡位置的位移x的关系式，画出小球运动的全过程中速度随振动位移变化的v﹣x图象。
【答案】（1）a．
；b．见解析。（2）a．见解析。b．
；
【解析】
（1）a．对小球，由平衡条件mg＝ks。
b．设小球偏离平衡位置x时的回复力为F回＝mg﹣k（s+x）＝﹣kx，故小球做简谐运动。
（2）a．重力势能EpG＝﹣mgx
以平衡位置处弹性势能为0，从平衡位置（弹簧伸长量为s）到坐标为x处（弹簧伸长量为s+x），根据弹簧弹力特点做出F﹣x图线如图，弹簧弹力做功为
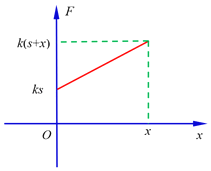
设x坐标处的弹性势能为
，由弹力做功与弹性势能变化量的关系可知
，即
得
重力势能和弹性势能的总和
。
b．小球在运动到平衡位置O点下方距离为
时的势能
小球在振幅处的动能为零，依据能量守恒定律有
可得，
由能量守恒定律
，即
，也即
，
整理得： 
故v﹣x图是椭圆。
