Question

【题目】如图所示的竖直平面内，相距为d的不带电平行金属板M、N水平固定放置，与灯泡L、开关S组成回路并接地，上极板M与其上方空间的D点相距h，灯泡L的额定功率与电压分别为PL、UL。带电量为q的小物体以水平向右的速度v0从D点连续发射，落在M板其电荷立即被吸收，M板吸收一定电量后闭合开关S，灯泡能维持正常发光。设小物体视为质点，重力加速度为g，金属板面积足够大，M板吸收电量后在板面均匀分布，M、N板间形成匀强电场，忽略带电小物体间的相互作用。

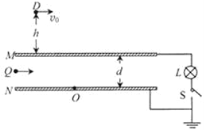
（1）初始时带电小物体落在M板上的水平射程为多少？

（2）单位时间发射小物体的个数为多少？

（3）闭合开关S后，带电粒子Q以水平速度从匀强电场左侧某点进入电场，并保持速度穿过M、N板之间。现若在M、N板间某区域加上方向垂直于纸面的匀强磁场，使Q在纸面内无论从电场左侧任何位置以某水平速度进入，都能到达N板上某定点O，求所加磁场区域为最小时的几何形状及位置。

Answer 1

【答案】（1）（2）（3）磁场的最小区域为圆，半径为；圆心为距0点的板间中心处．

【解析】

试题分析：（1）由题意知，在初始时M板不带电，带电小球在空间做平抛运动，设小物体到达M板时间为t1，水平射程为l1，则有：h=gt12；l1=v0t1

联立解是：；

（2）灯泡正常发光，金属板M、N间的电压为UL，由电容器原理可知，金属板M、N所带电量为定值，这时落到板M的电量全部流过灯泡，设流过灯泡的电流为IL，在时间t内流过灯泡的电量为QL，有：

PL=ILUL QL=ILt

设单位时间内发射小球的个数为n，则有：QL=nqt

联立以上各式解得：；

（3）闭合开关S后，M、N板间为匀强电场，Q进入后速度不变，则说明Q所受电场力与重力平衡，再进入磁场区域必做匀速圆周运动，以O点为坐标原点建立如图直角价坐标系xOy，

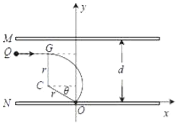
Q进入板间做匀速直线运动，设Q做匀速圆周运动的圆心为0，半径为r，OC与水平方向的夹角为θ，G点的坐标为（x，y），有x=-rcosθ； y=r+rsinθ

联立得：x2+（y-r）2=r2

则可知磁场在y轴左边的边界为半圆，要让该圆为量小，必有：

Q靠近M板进入磁场时做匀速圆周运动的轨迹为y轴右边的半圆，其方程为：

x2+（y-）2=（）2

Q从其它位置进入磁场做匀速圆周运动的轨迹不会超过y轴与此圆所围区域，故磁场在y轴右边区域最小的边界也为该半圆，则磁场的最小区域为圆，半径为；圆心为距0点的板间中心处．