题目内容
 (2007?浙江)如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂.现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点与金属球发生弹性碰撞.在平衡位置附近存在垂直于纸面的磁场.已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处.求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°.
(2007?浙江)如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂.现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点与金属球发生弹性碰撞.在平衡位置附近存在垂直于纸面的磁场.已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处.求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°.分析:先根据机械能守恒定律求出小球返回最低点的速度,然后根据动量守恒定律和机械能守恒定律求出碰撞后小球的速度,对速度表达式分析,求出碰撞n次后的速度表达式,再根据机械能守恒定律求出碰撞n次后反弹的最大角度,结合题意讨论即可.
解答:解:设小球m的摆线长度为l
小球m在下落过程中与M相碰之前满足机械能守恒:mgl(1-cosθ)=
mv02①
m和M碰撞过程是弹性碰撞,故满足:
mv0=MVM+mv1 ②
mv02=
mv12+
MVM2 ③
联立 ②③得:v1=
v0 ④
说明小球被反弹,且v1与v0成正比,而后小球又以反弹速度和小球M再次发生弹性碰撞,满足:
mv1=MVM1+mv2 ⑤
mv12=
mv22+
MVM12⑥
解得:
v2=
|v1| ⑦
整理得:
v2=-(
)2v0⑧
故可以得到发生n次碰撞后的速度:
vn=|(
)nv0|⑨
而偏离方向为450的临界速度满足:
mgl(1-cos450)=
mv临界2⑩
联立①⑨⑩代入数据解得,当n=2时,v2>v临界
当n=3时,v3<v临界
即发生3次碰撞后小球返回到最高点时与竖直方向的夹角将小于45°.
小球m在下落过程中与M相碰之前满足机械能守恒:mgl(1-cosθ)=
| 1 |
| 2 |
m和M碰撞过程是弹性碰撞,故满足:
mv0=MVM+mv1 ②
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立 ②③得:v1=
| m-M |
| m+M |
说明小球被反弹,且v1与v0成正比,而后小球又以反弹速度和小球M再次发生弹性碰撞,满足:
mv1=MVM1+mv2 ⑤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:
v2=
| m-M |
| m+M |
整理得:
v2=-(
| m-M |
| m+M |
故可以得到发生n次碰撞后的速度:
vn=|(
| m-M |
| m+M |
而偏离方向为450的临界速度满足:
mgl(1-cos450)=
| 1 |
| 2 |
联立①⑨⑩代入数据解得,当n=2时,v2>v临界
当n=3时,v3<v临界
即发生3次碰撞后小球返回到最高点时与竖直方向的夹角将小于45°.
点评:本题关键求出第一次反弹后的速度和反弹后细线与悬挂点的连线与竖直方向的最大角度,然后对结果表达式进行讨论,得到第n次反弹后的速度和最大角度,再结合题意求解.

练习册系列答案
相关题目


 (2007?浙江)两屏幕荧光屏互相垂直放置,在两屏内分别去垂直于两屏交线的直线为x和y轴,交点O为原点,如图所示.在y>0,0<x<a的区域有垂直于纸面向内的匀强磁场,在y>0,x>a的区域有垂直于纸面向外的匀强磁场,两区域内的磁感应强度大小均为B.在O点出有一小孔,一束质量为m、带电量为q(q>0)的粒子沿x周经小孔射入磁场,最后打在竖直和水平荧光屏上,使荧光屏发亮.入射粒子的速度可取从零到某一最大值之间的各种数值.已知速度最大的粒子在0<x<a的区域中运动的时间与在x>a的区域中运动的时间之比为2:5,在磁场中运动的总时间为7T/12,其中T为该粒子在磁感应强度为B的匀强磁场中做圆周运动的周期.试求两个荧光屏上亮线的范围(不计重力的影响).
(2007?浙江)两屏幕荧光屏互相垂直放置,在两屏内分别去垂直于两屏交线的直线为x和y轴,交点O为原点,如图所示.在y>0,0<x<a的区域有垂直于纸面向内的匀强磁场,在y>0,x>a的区域有垂直于纸面向外的匀强磁场,两区域内的磁感应强度大小均为B.在O点出有一小孔,一束质量为m、带电量为q(q>0)的粒子沿x周经小孔射入磁场,最后打在竖直和水平荧光屏上,使荧光屏发亮.入射粒子的速度可取从零到某一最大值之间的各种数值.已知速度最大的粒子在0<x<a的区域中运动的时间与在x>a的区域中运动的时间之比为2:5,在磁场中运动的总时间为7T/12,其中T为该粒子在磁感应强度为B的匀强磁场中做圆周运动的周期.试求两个荧光屏上亮线的范围(不计重力的影响).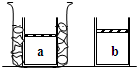 (2007?浙江)如图所示,质量为m的活塞将一定质量的气体封闭在气缸内,活塞与气缸之间无摩擦.a态是气缸放在冰水混合物中气体达到的平衡状态,b态是气缸从容器中移出后,在室温(27°C)中达到的平衡状态.气体从a态变化到b态的过程中大气压强保持不变.若忽略气体分子之间的势能,下列说法正确的是( )
(2007?浙江)如图所示,质量为m的活塞将一定质量的气体封闭在气缸内,活塞与气缸之间无摩擦.a态是气缸放在冰水混合物中气体达到的平衡状态,b态是气缸从容器中移出后,在室温(27°C)中达到的平衡状态.气体从a态变化到b态的过程中大气压强保持不变.若忽略气体分子之间的势能,下列说法正确的是( ) (2007?浙江)如图所示,LOO′L′为一折线,它所形成的两个角∠LOO′和∠OO′L′均为45°.折线的右边有一匀强磁场,其方向垂直OO′的方向以速度v做匀速直线运动,在t=0时刻恰好位于图中所示的位置.以逆时针方向为导线框中电流的正方向,在下面四幅图中能够正确表示电流-时间(I-t)关系的是(时间以l/v为单位)( )
(2007?浙江)如图所示,LOO′L′为一折线,它所形成的两个角∠LOO′和∠OO′L′均为45°.折线的右边有一匀强磁场,其方向垂直OO′的方向以速度v做匀速直线运动,在t=0时刻恰好位于图中所示的位置.以逆时针方向为导线框中电流的正方向,在下面四幅图中能够正确表示电流-时间(I-t)关系的是(时间以l/v为单位)( )