题目内容
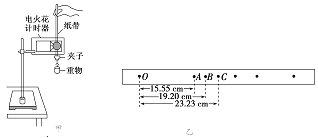
【题目】如图甲所示,一质量为![]() 小物块在水平面上A点处于静止状态,小物块与水平地面间的动摩擦因数为0.2,水平面右侧连有一半径为
小物块在水平面上A点处于静止状态,小物块与水平地面间的动摩擦因数为0.2,水平面右侧连有一半径为![]() 、竖直平面内的光滑半圆轨道,B为半圆轨道最低点,C为圆上与圆心等高点,D为轨道最高点。现用一水平向右的力F作用在小物块上,
、竖直平面内的光滑半圆轨道,B为半圆轨道最低点,C为圆上与圆心等高点,D为轨道最高点。现用一水平向右的力F作用在小物块上,![]() 随时间
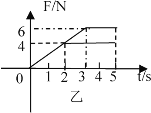
随时间![]() 的变化关系如乙图,
的变化关系如乙图,![]() 时小物块达到B点,此时撤去F。已知最大静摩擦力等于滑动摩擦力,
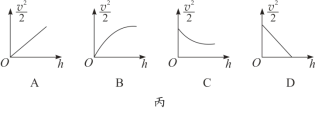
时小物块达到B点,此时撤去F。已知最大静摩擦力等于滑动摩擦力,![]() ,下列说法正确的是( )
,下列说法正确的是( )


A.![]() 时小物块速度为
时小物块速度为![]() B.小物块经过B点时对支持面的压力等于
B.小物块经过B点时对支持面的压力等于![]()
C.小物块能够到达圆轨道最高点DD.小滑块在运动中两次经过B点
【答案】D
【解析】
在![]() 图中做出摩擦力随时间变化图像如下图所示
图中做出摩擦力随时间变化图像如下图所示
A.![]() 内合力的冲量
内合力的冲量
![]()
解得
![]()
故A错误;
B.在B点有
![]()
得
![]()
根据牛顿第三定律可知,压力为51.25N,故B错误;
C.在轨道最高点的最小速度
![]()
假设从B点出发恰好能沿光滑轨道到达B点,根据机械能守恒得
![]()
得
![]()
因为在B点实际速度为
![]()
所以不能达到最高点,故C错误;
D.如果小物块以速度
![]()
沿有支撑物的轨道上升,可以达到高度
![]()
解得
![]()
所以小物块在达到C点之前速度变为0而随后沿轨道返回,故D正确。
故选D。

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目