题目内容
12. 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中,场强为E,一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,已知场强大小E<$\frac{mg}{q}$,不计空气阻力,则
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中,场强为E,一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,已知场强大小E<$\frac{mg}{q}$,不计空气阻力,则(1)物块在运动过程中摩擦力做的功是多少?
(2)证明物块离开C点落回到水平面的水平射程与场强大小E和质量m均无关.
分析 (1)物块恰能通过圆弧最高点C,由重和电场力的合力提供向心力,根据牛顿第二定律求出物块通过最高点C时的速度;物块在运动过程中,重力做负功,电场力做正功,摩擦力做负功,根据动能定理求解克服摩擦力做的功;
(2)物块离开半圆形轨道后做类平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由运动学公式即可证明.
解答 解:(1)物块恰能通过圆弧最高点C,圆弧轨道此时与物块间无弹力作用,物块受到的重力和电场力提供向心力,则有:
mg-Eq=m$\frac{{v}_{C}^{2}}{R}$…①
解得:vC=$\sqrt{R(g-\frac{qE}{m})}$…②
物块在由A运动到C的过程中,设物块克服摩擦力做的功Wf,根据动能定理有:Eq•2R-Wf-mg•2R=$\frac{1}{2}$m${v}_{C}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$…③
解得:Wf=$\frac{1}{2}m{v}_{0}^{2}$+$\frac{5}{2}$(Eq-mg)R…④
(2)物块离开半圆形轨道后做类平抛运动,设水平位移为s,则有:
s=vCt…⑤
2R=$\frac{1}{2}$(g-$\frac{qE}{m}$)t2…⑥
由⑤⑥联立解得:
s=2R…⑦
因此,物块离开轨道落回水平面的水平距离与场强大小E无关,大小为2R.
答:(1)物块在运动过程中克服摩擦力做的功是$\frac{1}{2}m{v}_{0}^{2}$+$\frac{5}{2}$(Eq-mg)R.
(2)证明见上.
点评 本题是向心力与动能定理、平抛运动等等知识的综合,关键要抓住物块恰能通过最高点C的临界条件,求出临界速度.

练习册系列答案
相关题目
3.物体静止在斜面上,下列说法不正确的是( )
| A. | 物体对斜面的压力和斜面对物体的支持力均属于弹力 | |
| B. | 物体对斜面的摩擦力和斜面对物体的摩擦力是一对平衡力 | |
| C. | 物体所受重力和斜面对物体的作用力是平衡力 | |
| D. | 物体所受重力可以分解为沿斜面向下的力和对斜面的压力 |
7. 如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )
 如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )| A. | 保持S闭合,将N板向下移,则P点的电势升高 | |
| B. | 保持S闭合,将N板向下移,则点电荷的电势能增大 | |
| C. | 将S断开,使N板向下移,则P点的电势减小 | |
| D. | 将S断开,使N板向下移,则点电荷的电势能减小 |
4.下列说法正确的是( )
| A. | 电容器是一种储存电荷的装置 | B. | 避雷针是用来防止静电的 | ||
| C. | 电感器应用了电流的热效应 | D. | 电磁炉应用了电磁感应现象 |
1.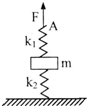 两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
 两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )| A. | 物体比施加F前高$\frac{mg}{{k}_{2}}$ | B. | A点比施加F前高$\frac{mg}{{k}_{1}}$ | ||
| C. | F<mg | D. | F>mg |
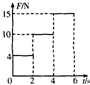 质量m=2.5kg的物体静止在粗糙的水平面上,在如图所示的水平拉力F作用下开始运动,则6s末物体的速度大小为多少?(已知物体与水平面间动摩擦因数0.2,g取10m/s2)
质量m=2.5kg的物体静止在粗糙的水平面上,在如图所示的水平拉力F作用下开始运动,则6s末物体的速度大小为多少?(已知物体与水平面间动摩擦因数0.2,g取10m/s2) 如图所示,光滑球重10N,球的半径20cm,绳的一端与球面上C点相连,AC的延长线经过圆心,使球靠在墙上而静止,绳子长20cm,求:
如图所示,光滑球重10N,球的半径20cm,绳的一端与球面上C点相连,AC的延长线经过圆心,使球靠在墙上而静止,绳子长20cm,求: