题目内容
2.处于静止状态的x原子核,经历一次α衰变后变成质量为M的Y原子核.放出的α粒子垂直射入磁感应强度为B的匀强磁场,测得其做匀速圆周运动的半径为r.已知α粒子的质量为m,电荷量为q,求此衰变过程的质量亏损.分析 根据带电粒子在匀强磁场中洛伦兹力提供向心力,求得α粒子的速度,再结合动量守恒定律和质能方程即可求得衰变过程中的质量亏损.
解答 解:令v表示α粒子的速度,由洛论兹力和牛顿定律可得qvB=$\frac{m{v}^{2}}{r}$
令v'表示衰变后剩余核的速度,在考虑衰变过程中系统的动量守恒时,因为亏损质量很小,可不予考虑,由动量守恒可知
Mv'=mv
在衰变过程中,α粒子和剩余核的动能来自于亏损质量.
即△m•c2=$\frac{1}{2}$Mv'2+$\frac{1}{2}$mv2
解得△m=$\frac{(M+m){q}^{2}{B}^{2}{r}^{2}}{2Mm{C}^{2}}$
答:在衰变过程中的质量亏损$\frac{(M+m){q}^{2}{B}^{2}{r}^{2}}{2Mm{C}^{2}}$.
点评 该题将带电粒子在磁场中的圆周运动与动量守恒定律和质能方程结合在一起,要理清它们之间的关系,确定要使用的公式.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
12.两个大小相同、带等量电荷的导体小球A和B库伦力为F.另一个不带电相同小球C,先与A接触,再与B接触,然后移开,这时A和B之间的作用力为F′,则F与F′之比可能为( )
| A. | 8:3 | B. | 8:1 | C. | 1:8 | D. | 4:1 |
13.科技活动小组的同学们为给西昌邛海湿地公园增加梦幻夜景做了一个小实验,将两盏发不同颜色单色光的灯A.B安装在水面下同一深度,结果发现A灯照亮的水面区域较大,以下说法正确的是( )
| A. | A光的折射率小于B光的折射率 | |
| B. | 在水中A光的传播速度小于B光的传播速度 | |
| C. | 在水中A光的传播速度等于B光的传播速度 | |
| D. | 在水中发生全反射时A光的临界角小于B光的临界角 |
10. 如图甲所示,理想变压器原、副线圈的匝数比为10:1,R1=20Ω,R2=30Ω,C为电容器.已知通过R1的正弦交流电如图乙所示,则下列表述正确的是( )
如图甲所示,理想变压器原、副线圈的匝数比为10:1,R1=20Ω,R2=30Ω,C为电容器.已知通过R1的正弦交流电如图乙所示,则下列表述正确的是( )
 如图甲所示,理想变压器原、副线圈的匝数比为10:1,R1=20Ω,R2=30Ω,C为电容器.已知通过R1的正弦交流电如图乙所示,则下列表述正确的是( )
如图甲所示,理想变压器原、副线圈的匝数比为10:1,R1=20Ω,R2=30Ω,C为电容器.已知通过R1的正弦交流电如图乙所示,则下列表述正确的是( )| A. | 交流电的频率为0.02 Hz | B. | 原线圈输入电压的最大值为282V | ||
| C. | 电阻R2的电功率约为6.67 W | D. | 通过R3的电流始终为零 |
17.一质量为m的人站在电梯中,电梯加速上升,加速度大小为$\frac{g}{2}$,则人对电梯底部的压力为( )
| A. | mg | B. | $\frac{2mg}{3}$ | C. | $\frac{3mg}{2}$ | D. | $\frac{mg}{2}$ |
14.下列关于质点的说法中正确的是( )
| A. | 只有体积很小的物体才能看成是质点 | |
| B. | 只有质量很小的物体才能看成是质点 | |
| C. | 质点一定代表一个小球 | |
| D. | 当物体大小远小于运动的距离时,可以把物体看成质点 |
11.已知万有引力常量,利用下列哪组,可以计算出地球的质量( )
| A. | 卫星绕地球做匀速圆周运动的线速度和周期 | |
| B. | 卫星绕地球做匀速圆周运动的轨道半径和周期 | |
| C. | 卫星绕地球做匀速圆周运动的轨道半径和线速度 | |
| D. | 卫星绕地球做匀速圆周运动的周期和角速度 |
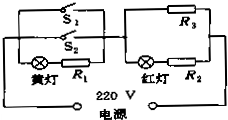 如图所示是电饭煲的电路图,S1是一个控温开关,手动闭合后,当此开关温度达到居里点(103℃)时,会自动断开.S2是一个自动控温开关,当温度低于70℃时会自动闭合;温度高于80℃时,会自动断开.红灯是加热时的指示灯,黄灯是保温时的指示灯.分流电阻R1=R2=500Ω,计算加热电阻丝R3=50Ω,两灯电阻不计.
如图所示是电饭煲的电路图,S1是一个控温开关,手动闭合后,当此开关温度达到居里点(103℃)时,会自动断开.S2是一个自动控温开关,当温度低于70℃时会自动闭合;温度高于80℃时,会自动断开.红灯是加热时的指示灯,黄灯是保温时的指示灯.分流电阻R1=R2=500Ω,计算加热电阻丝R3=50Ω,两灯电阻不计. 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中,场强为E,一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,已知场强大小E<$\frac{mg}{q}$,不计空气阻力,则
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中,场强为E,一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,已知场强大小E<$\frac{mg}{q}$,不计空气阻力,则