题目内容
【题目】如图所示，在xOy平面内存在着沿y轴方向的匀强电场，电场强度E=0．2V/m。
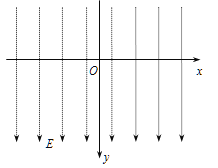
（1）现把比荷
=50C/kg带正电的粒子在原点O处由静止释放，不计粒子所受的重力。求经过时间t1=0．2s时带电粒子的位置坐标（x，y）。
（2）保持电场不变，在此空间加一垂直于xOy平面向里的匀强磁场，感应强度B=0．1T（图中末画出），仍把比荷=50C/kg带正电的粒子在原点处由静止释放，不计粒子所受的重力，粒子将在复合场中做滚轮线运动。求：
①带电粒子所能达到最大速度vmax；
②带电粒子在运动过程中离开x轴的最大距离H。
【答案】（1）（0，0．2m）；（2）①4m/s；②0．8m。
【解析】
试题分析：（1）由题意知，粒子在电场中沿y轴负方向做匀加速直线运动。
所以0．2s时粒子的位置坐标为（0，0．2m）
（2）解法一：运动的合成与分解
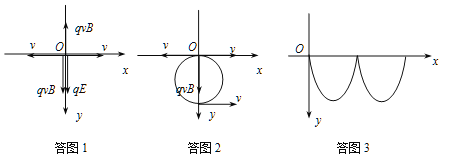
①如答图1所示，可以将初速度0分解为水平向左的v和水平向右的v，
其中v满足：
这样，粒子的运动可以看成以水平向右v为速度的匀速直线运动和水平向左v为初速度的匀速圆周运动的合成，如答图2所示。其运动轨迹为滚轮线，如答图3。
当两个分运动速度方向相同时，合速度最大。
带电粒子所能达到最大速度
②粒子离开x轴的最大距离即为圆周运动的直径。
（2）解法二：微元法
分析：粒子进入复合场后只受两个力作用，一个是电场力，一个是洛仑兹力，洛仑兹力不做功，当粒子有最大速度时，也就是粒子离开x轴有最大距离时。
设粒子离开x轴有最大距离H，某时刻粒子沿y轴方向的速度为vy，在极短的时间Δt内有：
（沿x方向运用动量定理）
在时间T内进行累加有下列表达式：
得：
①
从能量角度有：
②
联立方程①②可得：
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
