��Ŀ����
����Ŀ����ͼ��ʾ������M=1kg��ľ�徲ֹ�ڴֲڵ�ˮƽ�����ϣ�ľ��������Ķ�Ħ������![]() ����ľ�����˷���һ������m=1kg����С���Ժ��Ե����飬������ľ���Ķ�Ħ������
����ľ�����˷���һ������m=1kg����С���Ժ��Ե����飬������ľ���Ķ�Ħ������![]() ��ȡg=10m/s2������
��ȡg=10m/s2������
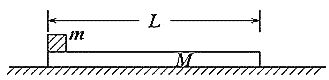
��1����������һ��ˮƽ���ҵij��ٶȣ���СΪ6m/s��Ϊʹ������ľ�岻���룬��ľ�峤������Ϊ���٣�
��2����ľ�峤L=1m���������ϼ�һ��ˮƽ���ҵĺ���F=8N�������ʱ�������˶���ľ����Ҷˣ�
��3������������ʩ��һ����С���㿪ʼ�������ӵ�ˮƽ���ҵ���F��ͨ�������ͼ��������ͼ�л��������ܵ�ľ���Ħ����f2������F��С�仯��ͼ����ľ���㹻������
���𰸡���1��L=3m��2��t=1s��3��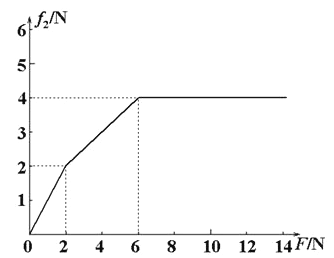
�����������������Ҫʹ���߲����룬�ٽ������ǵ������˶���ľ����Ҷ�ʱ�����ٶ�������ù�����������Ħ�����������������˶���ľ����Ħ�������������ȼ���ֱ���˶���������Ե����λ�Ʋ����ľ��ij��ȣ��ݴ���ʽ��⣻����ţ�ٵڶ��������ľ���ľ��ļ��ٶȣ������˶���ľ����Ҷ�ʱ��������ľ���λ��֮����ڰ峤����λ�ƹ�ʽ��ʽ���ʱ�䣮��ľ����Ҷ�ʩ��һ����С���㿪ʼ�������ӵ�ˮƽ�������Fʱ������ľ���������״̬������ƽ��������ţ�ٵڶ���������������ܵ�Ħ����f��F�Ĺ�ϵ������ͼ��
��1��Ҫʹ���߲����룬�ٽ������ǵ������˶���ľ����Ҷ�ʱ�����ٶ���ȣ�
�ù�����������Ħ�����������������˶���ľ����Ħ�������������ȼ���ֱ���˶���������Ե����λ�Ʋ����ľ��ij��ȣ�
����ļ��ٶ�![]()
ľ��ļ��ٶ�![]()
�������ٶ����ʱ�� ![]() �����
�����![]() ����ĩ�ٶ�
����ĩ�ٶ�![]()
�����λ��Ϊ�� ![]() ��ľ���λ��Ϊ
��ľ���λ��Ϊ![]() ��ľ��ij���
��ľ��ij���![]() ��
��
�������![]()
��2�����������ţ�ٵڶ����ɿɵ�![]()
��ľ�����ţ�ٵڶ����ɿɵ�![]()
![]()
�������![]()

��3��������ľ��֮������Ħ������ ![]()
ľ�������֮������Ħ������ ![]()
��![]() ʱ��ľ���뻬�鶼���־�ֹ��
ʱ��ľ���뻬�鶼���־�ֹ�� ![]()
��M��m���˶����������߸�Ҫ��Ի���ʱ�����ʱ��������СΪ![]() ������ţ�ٵڶ����ɵã���m��
������ţ�ٵڶ����ɵã���m�� ![]() �������壺
�������壺 ![]()
�������![]() �����Ե�
�����Ե�![]() ʱ��M��m��Ծ�ֹ
ʱ��M��m��Ծ�ֹ
���У������壺 ![]() �������飺
�������飺 ![]()
���� ![]()
��6N��Fʱ��m���M��������ʱĦ����![]()
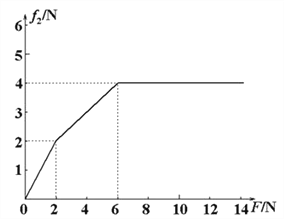
����f2������F��С�仯��ͼ����ͼ��ʾ��

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�