Question

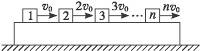
如图5-2-11所示，一块足够长的木板，放在光滑的水平面上，在木板上自左向右放着序号是1、2、3、…n的木块，所有木块的质量均为m，与木板间的动摩擦因数都相同.开始时，木板静止不动，第 1、2、3、…n号木块的初速度分别是v₀、2v₀、3v₀、…nv₀，方向都向右，木板的质量与所有的木块的总质量相同，最终所有木块与木板以共同的速度匀速运动.设木块之间均无相互碰撞，木板足够长，求：

图5-2-11

（1）所有木块与木板一起匀速运动的速度v_n；

（2）第1号木块与木板刚好相对静止时的速度v₁；

（3）通过分析与计算说明第k号（k＜n）木块的最小速度v_k.

Answer 1

解析：(1)以n块木块和木板为研究对象,在全过程中,该系统动量守恒有:m(v₀+2v₀+…+nv₀)=(nm+nm)v_n,解得v_n=v₀.

(2)由于每个木块与木板间的滑动摩擦力相同,在第1号木块由速度v₀减为与木板刚好相对静止时速度v₁过程中,对木板,其动量增量Δp₁=nm·v₁;对n个木块动量的增量Δp₂=n［m·(v₁-v₀)］,由n个木块与木板构成的系统动量守恒,则Δp₁+Δp₂=0,解以上各式得v₁=.

(3)当第k号木块与木板相对静止时,速度最小为v_k,对n个木块与木板构成的系统,初始总动量p₁=m(v₀+2v₀+…+nv₀),此时总动量p₂=k(mv_k)+nm·v_k+p,式中p为此时从第k+1个木块到第n个木块的总动量.由于后面(n-k)个木块每个木块在相同时间内损失的动量都相同,且为m(kv₀-v_k),则p=［(k+1)+(k+2)+…+n］mv₀-(n-k)m(kv₀-v_k),根据系统总动量守恒,得p₁=p₂,解以上各式得v_k=v₀.

答案：(1)v₀  (2)  (3)v₀