题目内容
11.在离地125米处小球A由静止开始下落,与此同时在A的正下方地面上以初速度v0竖直上抛另一个小球B.(1)若A、B两同时落地,求A球落地时间t和B球上抛的最大高度H.
(2)若A、B恰好在B上抛的最高点相遇,求B球上抛的初速度V0.
(3)若要保证B在上升阶段能与A相遇,则B球上抛的初速度V0应满足什么条件?
分析 (1)A球做自由落体运动,B球做竖直上升运动,根据同时落地的条件分析即可;
(2)相遇时在最高点,根据竖直上抛和自由落体运动的特点与公式即可求出B的速度;
(3)在上升过程中到达最高点相遇求的此时速度即可判断.
解答 解:(1)A球落地的时间:$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×125}{10}}=5$s
B球做竖直上抛运动,上升的时间与下落的时间相等,所以下落的时间:${t}_{1}=\frac{1}{2}t=\frac{1}{2}×5=2.5$s
B球下落的高度:$H=\frac{1}{2}g{t}_{1}^{2}=\frac{1}{2}×10×2.{5}^{2}=31.25$m
即B竖直上抛的最大高度是31.25m
(2)若A、B恰好在B上抛的最高点相遇,设相遇的时间是t0,则A与B相遇时:${v}_{0}{t}_{0}-\frac{1}{2}g{t}_{0}^{2}+\frac{1}{2}g{t}_{0}^{2}=h$;
v0-gt0=0
代入数据得:t0=3.53s
所以:v0=gt0=10×3.53=35.3m/s
(3)若要保证B在上升阶段能与A相遇,设相遇的时间是t0′,则A与B相遇时:${v}_{0}{t}_{0}′-\frac{1}{2}g{t′}_{0}^{2}+\frac{1}{2}g{t′}_{0}^{2}=h$;
v0-gt0′>0
代入数据得:v0′>35.3m/s
答:(1)若A、B两同时落地,A球落地时间t是5s,B球上抛的最大高度H是31.5m.
(2)若A、B恰好在B上抛的最高点相遇,B球上抛的初速度等于35.3m/s.
(3)若要保证B在上升阶段能与A相遇,则B球上抛的初速度V0应大于35.3m/s
点评 本题关键是明确竖直上抛运动和自由落体运动的运动性质,然后根据运动学公式列式求解.

| A. | 磁感线从磁体的N极出发,终止于S极 | |
| B. | 小磁针N极受磁场力的方向就是该处磁感应强度的方向 | |
| C. | 磁场中垂直穿过某一面的磁感线条数就叫做穿过这个面的磁通量 | |
| D. | 通电导线所受安培力F必须垂直磁感应强度B、电流I,但B、I可以不相互垂直 |
 某同学在做“探究弹力和弹簧伸长的关系”的实验时,所用实验装置如图1所示,所用的钩码每只质量都是30g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,并将数据填在表中.(实验中弹簧始终未超过弹性限度,取g=10m/s2)
某同学在做“探究弹力和弹簧伸长的关系”的实验时,所用实验装置如图1所示,所用的钩码每只质量都是30g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,并将数据填在表中.(实验中弹簧始终未超过弹性限度,取g=10m/s2)| 钩码质量/g | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长/cm | 6.00 | 7.00 | 8.00 | 9.00 | 10.00 | 11.00 |
(2)图线跟横轴交点的物理意义是弹簧的原长;当悬挂钩码质量为90g时,弹簧被拉长了3cm;该弹簧的劲度系数k=30N/m.
| A. | 磁体的重心处 | B. | 磁体的某一磁极处 | ||
| C. | 磁体重心的北侧 | D. | 磁体重心的南侧 |
| A. | 时间代表的时间比较长,时刻代表的时间比较短 | |
| B. | 时间在时间轴上是一条线段,时刻在时间轴上是一个点 | |
| C. | 时间是一个状态量,时刻是一个过程量 | |
| D. | 时间是标量,时刻是矢量 |
 如图,O、A、B为同一斜面内的三个点,OB沿斜面向下,∠BOA=60°,0B=$\frac{3}{2}$OA.将一质量为m的小球以初速度v0自O点平行斜面水平向右抛出,小球在运动过程中恰好通过A点.使此小球带电,电荷量为q(q>0),同时加一匀强电场.场强方向与△OAB所在平面平行,现从O点以同样的速率沿某一平行斜面方向抛出此带电小球,该小球也恰好通过了A点,到达A点时的动能是初动能的3倍;若该小球从O点以同样的速率沿另一平行斜面方向抛出,恰好通过B点,且到达B点的动能为初动能的6倍,重力加速度大小为g.固定光滑斜面的倾角θ=30°,求:
如图,O、A、B为同一斜面内的三个点,OB沿斜面向下,∠BOA=60°,0B=$\frac{3}{2}$OA.将一质量为m的小球以初速度v0自O点平行斜面水平向右抛出,小球在运动过程中恰好通过A点.使此小球带电,电荷量为q(q>0),同时加一匀强电场.场强方向与△OAB所在平面平行,现从O点以同样的速率沿某一平行斜面方向抛出此带电小球,该小球也恰好通过了A点,到达A点时的动能是初动能的3倍;若该小球从O点以同样的速率沿另一平行斜面方向抛出,恰好通过B点,且到达B点的动能为初动能的6倍,重力加速度大小为g.固定光滑斜面的倾角θ=30°,求: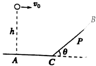 如图所示,一个小球从高h=10m处水平速度v0=10m/s,撞在倾角θ=45°的斜面上的P点,已知AC=5m(g=10m/s2),求:P、C之间的距离.
如图所示,一个小球从高h=10m处水平速度v0=10m/s,撞在倾角θ=45°的斜面上的P点,已知AC=5m(g=10m/s2),求:P、C之间的距离.