Question

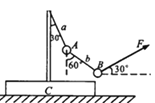
【题目】如图所示，质量为M的木板C放在水平地面上，固定在C上的竖直轻杆的顶端分别用细绳a和b连接小球A和小球B，小球A、B的质量均为m，当与水平方向成30°角的力F作用在小球B上时，A、B、C处于静止状态，且此时绳a、b与竖直方向的夹角分别为30°和60°，则下列判断正确的是( )

A. 力F的大小为mg

B. 地面对C的支持力等于（M＋2m）g

C. 地面对C的摩擦力大小为mg

D. 若保持A、B两球静止，且F方向可调，则F的最小值为mg

Answer 1

【答案】AD

【解析】以B为研究对象，分析受力，水平方向受力平衡，则有：Fcos30°=Tbcos30°，得：Tb=F
竖直方向受力平衡，则：Fsin30°+Tbsin30°=mg，得F=mg，故A正确；以ABC整体为研究对象受力分析，竖直方向：N+Fsin30°=（M+2m）g，可见N小于（M+2m）g，故B错误；以ABC整体为研究对象受力分析，水平方向：f=Fcos30°=mgcos30°=mg，故C错误；
当拉力F的方向与b绳子垂直时，拉力F最小．最小为：Fmin＝mgsin60°＝mg，故D正确；故选AD.