题目内容
11. 两重叠在一起的滑块,置于固定的倾角为θ的斜面上,如图所示,滑块A、B的质量分别为m1、m2,A与斜面间的动摩擦因数为μ1,B与A的动摩擦因数为μ2.已知两滑块都从斜面由静止以相同的加速度滑下,滑块B受到的摩擦力为( )
两重叠在一起的滑块,置于固定的倾角为θ的斜面上,如图所示,滑块A、B的质量分别为m1、m2,A与斜面间的动摩擦因数为μ1,B与A的动摩擦因数为μ2.已知两滑块都从斜面由静止以相同的加速度滑下,滑块B受到的摩擦力为( )| A. | 等于零 | B. | 方向沿斜面向上 | ||
| C. | 大小等于μ1m2gcosθ | D. | 大小等于μ2m2gcosθ |
分析 A、B叠在一起,A在B上.两滑块都从静止开始以相同的加速度沿斜面滑下,可以先用整体法求共同的加速度,然后在对A单独分析即可求得A所受摩擦力.
解答  解:对A、B整体受力分析如图所示,在沿斜面方向由牛顿第二定律得:
解:对A、B整体受力分析如图所示,在沿斜面方向由牛顿第二定律得:
(m+M)gsinθ-F=(m+M)a…①
且滑动摩擦力为:F=μ1(m+M)gcosθ…②
得a=g(sinθ-μ1cosθ)
假设A受的摩擦力FA方向沿斜面向下,A受重力、B的支持力和摩擦力,在沿斜面方向上由牛顿第二定律得:
mgsinθ+FA=ma…③
由以上三式解得:FA=-μ1mgcosθ,
负号表示FA方向与假设的方向相反,即B对A的摩擦力沿斜面向上.
根据牛顿第三定律,A对B的摩擦力方向沿斜面向下,故C正确; 故A、B、D错误.
故选:C.
点评 本题关键是先对整体受力分析,根据牛顿第二定律求解出加速度,然后再隔离出物体A,运用牛顿第二定律求解AB间的内力

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
1.关于阻尼振动说法正确的是( )
| A. | 振幅逐渐减小,但是周期不变 | B. | 振幅逐渐减小,周期也逐渐减小 | ||
| C. | 振幅不变,周期不变 | D. | 振幅不变,周期逐渐变小 |
2. 如图所示,在竖直方向上有四条间距为L=0.5m的水平虚线L1,L2,L3,L4,在L1L2之间,L3L4之间存在匀强磁场,大小均为1T,方向垂直于纸面向里.现有一矩形线圈abcd,长度ad=3L,宽度cd=L,质量为0.1kg,电阻为1Ω,将其从图示位置静止释放(cd边与L1重合),cd边经过磁场边界线L3时恰好做匀速直线运动,整个运动过程中线圈平面始终处于竖直方向,cd边水平,(g=10m/s2)则( )
如图所示,在竖直方向上有四条间距为L=0.5m的水平虚线L1,L2,L3,L4,在L1L2之间,L3L4之间存在匀强磁场,大小均为1T,方向垂直于纸面向里.现有一矩形线圈abcd,长度ad=3L,宽度cd=L,质量为0.1kg,电阻为1Ω,将其从图示位置静止释放(cd边与L1重合),cd边经过磁场边界线L3时恰好做匀速直线运动,整个运动过程中线圈平面始终处于竖直方向,cd边水平,(g=10m/s2)则( )
 如图所示,在竖直方向上有四条间距为L=0.5m的水平虚线L1,L2,L3,L4,在L1L2之间,L3L4之间存在匀强磁场,大小均为1T,方向垂直于纸面向里.现有一矩形线圈abcd,长度ad=3L,宽度cd=L,质量为0.1kg,电阻为1Ω,将其从图示位置静止释放(cd边与L1重合),cd边经过磁场边界线L3时恰好做匀速直线运动,整个运动过程中线圈平面始终处于竖直方向,cd边水平,(g=10m/s2)则( )
如图所示,在竖直方向上有四条间距为L=0.5m的水平虚线L1,L2,L3,L4,在L1L2之间,L3L4之间存在匀强磁场,大小均为1T,方向垂直于纸面向里.现有一矩形线圈abcd,长度ad=3L,宽度cd=L,质量为0.1kg,电阻为1Ω,将其从图示位置静止释放(cd边与L1重合),cd边经过磁场边界线L3时恰好做匀速直线运动,整个运动过程中线圈平面始终处于竖直方向,cd边水平,(g=10m/s2)则( )| A. | cd边经过磁场边界线L1时通过线圈的电荷量为0.5C | |
| B. | cd边经过磁场边界线L3时的速度大小为4m/s | |
| C. | cd边经过磁场边界线L2和L4的时间间隔为0.25s | |
| D. | 线圈从开始运动到cd边经过磁场边界线L4过程,线圈产生的热量为0.7J |
6.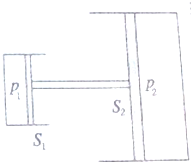 如图所示,两圆柱形气缸均水平固定,大小活塞光滑、面积分别为S2和S1,两活塞之间有水平杆连接,当小气缸内封闭气体压强为p1时,水平杆处于静止状态.求大气缸内所封闭气体的压强p2(设大气压为p0).
如图所示,两圆柱形气缸均水平固定,大小活塞光滑、面积分别为S2和S1,两活塞之间有水平杆连接,当小气缸内封闭气体压强为p1时,水平杆处于静止状态.求大气缸内所封闭气体的压强p2(设大气压为p0).
 如图所示,两圆柱形气缸均水平固定,大小活塞光滑、面积分别为S2和S1,两活塞之间有水平杆连接,当小气缸内封闭气体压强为p1时,水平杆处于静止状态.求大气缸内所封闭气体的压强p2(设大气压为p0).
如图所示,两圆柱形气缸均水平固定,大小活塞光滑、面积分别为S2和S1,两活塞之间有水平杆连接,当小气缸内封闭气体压强为p1时,水平杆处于静止状态.求大气缸内所封闭气体的压强p2(设大气压为p0).
16. 如图所示是一列简谐横波在t=0时刻的波形图.已知这列波沿x轴正方向传播,波速为20m/s,则在t=0.17s时该质点P( )
如图所示是一列简谐横波在t=0时刻的波形图.已知这列波沿x轴正方向传播,波速为20m/s,则在t=0.17s时该质点P( )
 如图所示是一列简谐横波在t=0时刻的波形图.已知这列波沿x轴正方向传播,波速为20m/s,则在t=0.17s时该质点P( )
如图所示是一列简谐横波在t=0时刻的波形图.已知这列波沿x轴正方向传播,波速为20m/s,则在t=0.17s时该质点P( )| A. | 速度沿-y方向,加速度沿+y方向 | B. | 速度沿+y方向,加速度沿-y方向 | ||
| C. | 速度和加速度均正在增大 | D. | 速度正在增大,加速度正在减少 |
 如图,两相同的光滑球分别用等长的绳子悬于同一点.此两球同时又支撑着一个等重量、等大的光滑球而处于平衡状态.求图中α (悬线与竖直线的夹角)与β(球心连线与竖直线的夹角)的关系.
如图,两相同的光滑球分别用等长的绳子悬于同一点.此两球同时又支撑着一个等重量、等大的光滑球而处于平衡状态.求图中α (悬线与竖直线的夹角)与β(球心连线与竖直线的夹角)的关系.