题目内容
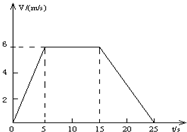
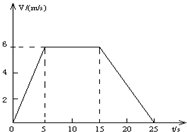 矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求:
矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求:
(1)升降机加速时的加速度;
(2)矿井的深度;
(3)升降机减速时体重为60千克的矿工对升降机的压力.
解:
(1)由图,在0-5s内,升降机加速上升,其加速度为a=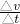 =
=
(2)矿井的深度等于图线与t轴所围“面积”,则矿井的深度h= =105m.
=105m.
(3)由图,在15-25s内,升降机减速上升,其加速度为大小a=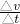 =
=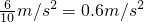 ,方向竖直向下.
,方向竖直向下.
以矿工为研究对象,根据牛顿第二定律得
mg-N=ma
得到,升降机对矿工的支持力N=mg-ma=60×(10-0.6)N=564N
则由牛顿第三定律得知,矿工对升降机的压力大小为N′=N=564N.
答:
(1)升降机加速时的加速度是1.2m/s2;
(2)矿井的深度是105m;
(3)升降机减速时体重为60千克的矿工对升降机的压力是564N.
分析:(1)根据速度图象的斜率等于物体的加速度,由数学知识求出升降机加速时的加速度;
(2)矿井的深度等于图线与t轴所围“面积”,由几何知识求出深度.
(3)根据斜率求出升降机减速时的加速度,由牛顿运动定律求出矿工对升降机的压力.
点评:根据速度-时间图象读出加速度和位移,是应掌握的基本能力.基础题,只要细心计算,不应失分.
(1)由图,在0-5s内,升降机加速上升,其加速度为a=
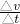 =
=
(2)矿井的深度等于图线与t轴所围“面积”,则矿井的深度h=
 =105m.
=105m.(3)由图,在15-25s内,升降机减速上升,其加速度为大小a=
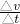 =
=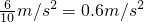 ,方向竖直向下.
,方向竖直向下.以矿工为研究对象,根据牛顿第二定律得
mg-N=ma
得到,升降机对矿工的支持力N=mg-ma=60×(10-0.6)N=564N
则由牛顿第三定律得知,矿工对升降机的压力大小为N′=N=564N.
答:
(1)升降机加速时的加速度是1.2m/s2;
(2)矿井的深度是105m;
(3)升降机减速时体重为60千克的矿工对升降机的压力是564N.
分析:(1)根据速度图象的斜率等于物体的加速度,由数学知识求出升降机加速时的加速度;
(2)矿井的深度等于图线与t轴所围“面积”,由几何知识求出深度.
(3)根据斜率求出升降机减速时的加速度,由牛顿运动定律求出矿工对升降机的压力.
点评:根据速度-时间图象读出加速度和位移,是应掌握的基本能力.基础题,只要细心计算,不应失分.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
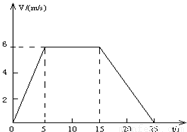
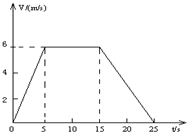 矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求:
矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求: