题目内容
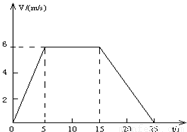
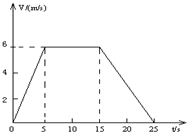
矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求:
(1)升降机加速时的加速度;
(2)矿井的深度;
(3)升降机减速时体重为60千克的矿工对升降机的压力.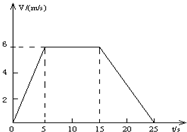
(1)升降机加速时的加速度;
(2)矿井的深度;
(3)升降机减速时体重为60千克的矿工对升降机的压力.

(1)由图,在0-5s内,升降机加速上升,其加速度为a=
| △v |
| △t |
| 6-0 |
| 5 |
(2)矿井的深度等于图线与t轴所围“面积”,则矿井的深度h=
| 10+25 |
| 2 |
(3)由图,在15-25s内,升降机减速上升,其加速度为大小a=
| △v |
| △t |
| 6 |
| 10 |
以矿工为研究对象,根据牛顿第二定律得
mg-N=ma
得到,升降机对矿工的支持力N=mg-ma=60×(10-0.6)N=564N
则由牛顿第三定律得知,矿工对升降机的压力大小为N′=N=564N.
答:
(1)升降机加速时的加速度是1.2m/s2;
(2)矿井的深度是105m;
(3)升降机减速时体重为60千克的矿工对升降机的压力是564N.

练习册系列答案
相关题目
 矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求:
矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求: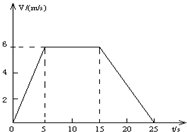 矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求:
矿井里的升降机,自井底由静止开始向上运动,其速度随时间的关系如图所示,已知25秒末升降机恰到达地面.求: