题目内容
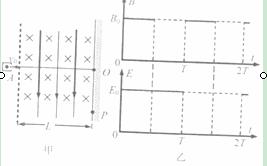
如图甲所示,’真空区域内有一粒子源A.能每隔T/2的时间间隔定时地沿AO方向向外发出一个粒子.虚线右侧为一有理想边界的相互正交的匀强电场和匀强磁场区域,离虚线距离为L的位置处有一荧光屏,粒子打到荧光屏上将使荧光屏上出现一个亮点。虚线和荧光屏相互平行,而AO与荧光屏相互垂直。如果某时刻粒子运动到虚线位置开始记时(记为t= 0).加上如图乙所示周期性变化的电、磁场,场强大小关系为![]() (其中
(其中![]() 为粒子到达虚线位置时的速度大小).发现t=3T/2时刻到达虚线位置的粒子在t=2T时刻到达荧光屏上的O点;在t=T/2时刻到达虚线位置的粒子打到荧光屏上的P点,且OP之间的距离为L/2,试根据以上条件确定,荧光屏上在哪些时刻,在什么位置有粒子到达?
为粒子到达虚线位置时的速度大小).发现t=3T/2时刻到达虚线位置的粒子在t=2T时刻到达荧光屏上的O点;在t=T/2时刻到达虚线位置的粒子打到荧光屏上的P点,且OP之间的距离为L/2,试根据以上条件确定,荧光屏上在哪些时刻,在什么位置有粒子到达?
解:由于t=3T/2时刻到达虚线位置的粒子在t=2T时刻到达荧光屏上的O点,而在t=3T/2——t=2T期间电场和磁场都为零,粒子沿直线运动到O点,说明粒子的重力不计(1分),故:
(1)t=0时刻进入的粒子受到的电场力和洛仑兹力平衡,故作匀速直线运动,在t=T/2时刻到达O点。(2分)
(2)t=T/2时刻进入的粒子只受电场力作用,作类平抛运动,t=T时刻到达P点,OP=L/2。(2分)
(3)(3分)t=T时刻进入的粒子只受洛仑兹力作用,则由前面的运动特点得:
![]() 或:
或:![]()
![]()
![]()
粒子在磁场中运动的周期为:![]()
设经过T/2时间,即3T/2时刻粒子运动到F点,设此过程中粒子转过的圆心角为θ,则:
![]()
以后粒子不受力作匀速直线运动打到Q点,则QO点间的距离为:
![]()
从A点到Q点所用的时间为:![]()
其中:![]() ,表明上面讨论正确。
,表明上面讨论正确。
故t=T时刻进入的粒子,在![]() 时刻到达Q点。
时刻到达Q点。
(4)t=3T/2时刻到达虚线位置的粒子做匀速直线运动在t=2T时刻到达荧光屏上的O点。
(5)(2分)以后重复,即:
t=2kT(k=0,1,2,3,……)时刻到达虚线位置的粒子,在t=(2k+1/2)T(k=0,1,2,3,……)时刻到达O点;
t=(2k+1/2)T(k=0,1,2,3,……)时刻到达虚线位置的粒子,在t=(2k+1)T(k=0,1,2,3,……)时刻到达P点;
在t=(2k+1)T(k=0,1,2,3,……)时刻到达虚线位置的粒子,在t=(2k+1)T+![]() (k=0,1,2,3,……)时刻到达Q点;
(k=0,1,2,3,……)时刻到达Q点;
在t=(2k+3/2)T(k=0,1,2,3,……)时刻到达虚线位置的粒子,在t=(2k+2)T(k=0,1,2,3,……)时刻到达O点。
 |


 某同学设想用带电粒子的运动轨迹做出“0”、“8”字样,首先,如图甲所示,在真空空间的竖直平面内建立直角坐标系
某同学设想用带电粒子的运动轨迹做出“0”、“8”字样,首先,如图甲所示,在真空空间的竖直平面内建立直角坐标系
