题目内容
 如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端
如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端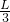 的c处,滑块刚好停在小车左端A处,设定平板车上表面各处粗糙程度相同.
的c处,滑块刚好停在小车左端A处,设定平板车上表面各处粗糙程度相同.
(1)求滑块和平板车间的摩擦因数;
(2)若平板车车速为2v0且保持不变,当滑块轻放到车面C处的同时对该滑块施加一个与车运动方向相同的恒力F,要保证滑块不能从车的左端A处掉下,恒力F大小应该满足什么条件?
(3)在(2)的情况下,力F取最小值,要保证滑块不从车上掉下,力F的作用时间应该在什么范围内?
解:(1)设小滑块受到的滑动摩擦力大小为f,则小物块产生的加速度a=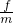 ,小物块运动的时间t=
,小物块运动的时间t=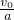 ,当小物块的速度和车的速度相同时有根据几何关系有:
,当小物块的速度和车的速度相同时有根据几何关系有:
 代入:a=
代入:a=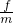 和t=
和t=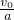 可得:
可得:

又因为f=μFN=μmg得动摩擦因数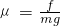 =
=
(2)设恒力F取最小值F′,滑块加速度为a1,此时滑块恰好达到车的左端,则滑块运动到车左端的时间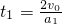 ①
①
由几何关系,有 2v0t1- =
=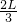 ②
②
由牛顿第二定律有:F′+f=ma1 ③
由①②③解得: ,
,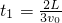
则恒力F大小应满足的条件是:F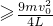
(3)力F取最小值,当滑块运动到车左端后,为使滑块恰不从右端画出,相对车先做匀加速运动(设运动加速度为a2,时间为t2),再做匀减速运动(设加速度大小为a3).到达车右端时,与车有共同速度,则有
F′-f=ma2 ④
f=ma3 ⑤
由几何关系有: ⑥
⑥
由④⑤⑥解得:
则力F的作用时间t应满足t1≤t≤t1+t2
即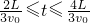
答:(1)滑块和平板车间的摩擦因数μ= ;
;
(2)若平板车车速为2v0且保持不变,当滑块轻放到车面C处的同时对该滑块施加一个与车运动方向相同的恒力F,要保证滑块不能从车的左端A处掉下,恒力F大小应该满足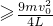
(3)在(2)的情况下,力F取最小值,要保证滑块不从车上掉下,力F的作用时间应该在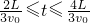 .
.
分析:(1)小滑块在滑动摩擦力的作用下向右加速,根据牛顿第二定律、运动学公式,结合几何关系列式求解;
(2)假设取最小值,则滑块恰好滑到最左端,再次根据牛顿第二定律、运动学公式和功能关系,结合几何关系列式求解;
(3)小滑块在平板车上先加速后减速,根据牛顿第二定律求加速度,根据运动学公式和几何关系列式联立求解恰好不掉下的临界时间
点评:本题关键是分析清楚物体受力后,根据牛顿第二定律求得各段的加速度,然后根据运动学公式结合几何关系列式求解.
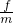 ,小物块运动的时间t=
,小物块运动的时间t=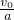 ,当小物块的速度和车的速度相同时有根据几何关系有:
,当小物块的速度和车的速度相同时有根据几何关系有: 代入:a=
代入:a=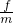 和t=
和t=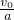 可得:
可得:
又因为f=μFN=μmg得动摩擦因数
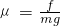 =
=
(2)设恒力F取最小值F′,滑块加速度为a1,此时滑块恰好达到车的左端,则滑块运动到车左端的时间
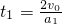 ①
①由几何关系,有 2v0t1-
 =
=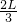 ②
②由牛顿第二定律有:F′+f=ma1 ③
由①②③解得:
 ,
,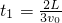
则恒力F大小应满足的条件是:F
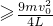
(3)力F取最小值,当滑块运动到车左端后,为使滑块恰不从右端画出,相对车先做匀加速运动(设运动加速度为a2,时间为t2),再做匀减速运动(设加速度大小为a3).到达车右端时,与车有共同速度,则有
F′-f=ma2 ④
f=ma3 ⑤
由几何关系有:
 ⑥
⑥由④⑤⑥解得:

则力F的作用时间t应满足t1≤t≤t1+t2
即
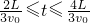
答:(1)滑块和平板车间的摩擦因数μ=
 ;
;(2)若平板车车速为2v0且保持不变,当滑块轻放到车面C处的同时对该滑块施加一个与车运动方向相同的恒力F,要保证滑块不能从车的左端A处掉下,恒力F大小应该满足
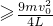
(3)在(2)的情况下,力F取最小值,要保证滑块不从车上掉下,力F的作用时间应该在
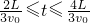 .
.分析:(1)小滑块在滑动摩擦力的作用下向右加速,根据牛顿第二定律、运动学公式,结合几何关系列式求解;
(2)假设取最小值,则滑块恰好滑到最左端,再次根据牛顿第二定律、运动学公式和功能关系,结合几何关系列式求解;
(3)小滑块在平板车上先加速后减速,根据牛顿第二定律求加速度,根据运动学公式和几何关系列式联立求解恰好不掉下的临界时间
点评:本题关键是分析清楚物体受力后,根据牛顿第二定律求得各段的加速度,然后根据运动学公式结合几何关系列式求解.

练习册系列答案
相关题目
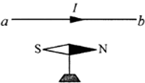 如图所示,在水平长直导线的正下方,有一只可以自由转动的小磁针.现给直导线通以由 a向b的恒定电流I,若地磁场的影响可忽略,则小磁针的N极将( )
如图所示,在水平长直导线的正下方,有一只可以自由转动的小磁针.现给直导线通以由 a向b的恒定电流I,若地磁场的影响可忽略,则小磁针的N极将( )| A、保持不动 | B、向下转动 | C、垂直纸面向里转动 | D、垂直纸面向外转动 |
 如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端
如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端
 如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0,做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端
如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0,做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端 如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v,做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端
如图所示,在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v,做匀速直线运动.某时刻将一质量为m,可视为质点的小滑块轻放到车面距右端 的c处,滑块刚好停在小车左端A处,设定平板车上表面各处粗糙程度相同.
的c处,滑块刚好停在小车左端A处,设定平板车上表面各处粗糙程度相同.