题目内容
(12分)如图所示，在光滑的桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3.0kg的金属块B，A的长度l=2.0m。B上有轻线绕过定滑轮与质量为mC=1.0kg的物块C相连，B与A之间的动摩擦因数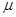
=0.10，最大静摩擦力可视为等于滑动摩擦力，忽略滑轮质量及与轴间的摩擦。起始时令各物体都处于静止状态，绳被拉直，B位于A的左端(如图)，然后放手，求经过多长时间t后B从A的右端脱离(设A的右端距滑轮足够远)(取g=10m/s2).
【答案】
t=4.0s
【解析】
试题分析：以桌面为参考系，令aA表示A的加速度，aB表示B、C的加速度，sA和sB分别表示t时间内A和B移动的距离，则由牛顿定律和匀加速运动的规律可得
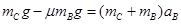
sB=
aBt2
sA=aAt2
sB－sA=l
由以上各式可得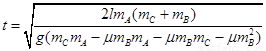 
=4.0s
考点：牛顿第二定律 匀变速直线运动规律 板块模型中相对运动的位移关系
练习册系列答案
相关题目
，式中k为恒量。框架上有一质量为m的金属棒水平放置，金属棒与光滑框架接触良好，离地高为h，磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放，棒沿框架向下运动。其它电阻不计，问：
（3）金属棒从释放到落地过程中在电子元件上消耗的电能多大？
等效电阻
，式中k为恒量。框架上有一质量为m的金属棒水平放置，金属棒与光滑框架接触良好，离地高为h，磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放，棒沿框架向下运动。其它电阻不计，问：
（3）金属棒从释放到落地过程中在电子元件上消耗的电能多大？
，S断开时，电压表示数为16V，S闭合时，电压表示数为10V，若电压表可视为理想的，则电源电动势和内电阻为多少？