题目内容
(12分)学校举行遥控赛车(可视为质点)比赛.比赛路径如图所示,赛车从起点A出发,赛车以额定功率P=2.0w沿水平直线轨道运动,过B点进入半径为R=0.4m的光滑竖直圆轨道,离开竖直圆轨道后继续沿光滑平直轨道运动,然后冲上光滑斜坡,最后从C点水平飞出落到水平轨道的D点.已知赛车质量m=0.1kg,,已知赛车在AB段运动中所受阻力f恒为0.2N.(取g=10m/s2)求:

(1)如果水平直线轨道AB足够长,求赛车运动过程中的最大速度Vm ;
(2)如果水平直线轨道AB长L=10m,要让赛车从竖直圆轨道E点通过,赛车从A点开始至少需工作多长时间;
(3) 如果赛车以最大速度冲过B点,绕过竖直圆轨道后到达C点,C点高度可调,那么赛车落地点D离飞出点C的最大水平位移多大?

(1)如果水平直线轨道AB足够长,求赛车运动过程中的最大速度Vm ;
(2)如果水平直线轨道AB长L=10m,要让赛车从竖直圆轨道E点通过,赛车从A点开始至少需工作多长时间;
(3) 如果赛车以最大速度冲过B点,绕过竖直圆轨道后到达C点,C点高度可调,那么赛车落地点D离飞出点C的最大水平位移多大?
(1) (2)v1=
(2)v1= m/s(3)
m/s(3)
 (2)v1=
(2)v1= m/s(3)
m/s(3)
试题分析:(1)赛车只能在水平轨道AB上加速,其它路段由于是光滑赛车的牵引力是不做功的,
所以当赛车在水平轨道AB上运动牵引力等于阻力时速度最大
 (2分)
(2分)(2)、设赛车到达B点的速度为v1,到达圆轨道最高点E的速度为v2,由牛顿第二定律及机械能守恒定律得:

 ①(1分)
①(1分)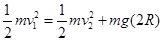 ②(2分)
②(2分)由于赛车以额定功率工作时间最短,为最短时间为t,根据动能定理:
 ③(2分)
③(2分) 由①②③可得t="1.5s" (1分)
v1=
 m/s
m/s( 由于 v1=
 m/s,在t="1.5s" 时赛车还未到达B点,所以③式成立,不说明不扣分 )
m/s,在t="1.5s" 时赛车还未到达B点,所以③式成立,不说明不扣分 )(3)设C点高度为h,赛车到达C点速度为v3 由机械能守恒可得:
 (2分)
(2分) 解得
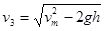
由平抛知识得:
 (1分)
(1分)水平位移
 (1分)
(1分)所以当时
 x最大 (1分),
x最大 (1分), 最大值是
 (1分)
(1分)点评:关键要将物体的运动分为三个过程,分析清楚各个过程的运动特点和受力特点,然后根据动能定理、平抛运动公式、向心力公式列式求解!

练习册系列答案
相关题目
 1,C板电势为
1,C板电势为


 光滑斜轨道。一质量为m=3kg小滑块从A点以v0=2m/s的初速度沿AB圆弧滑下,(斜轨道与水平轨道交接处有一段很小的圆弧,滑块经过交接处时与轨道的碰撞所引起的能量损失可以不计,
光滑斜轨道。一质量为m=3kg小滑块从A点以v0=2m/s的初速度沿AB圆弧滑下,(斜轨道与水平轨道交接处有一段很小的圆弧,滑块经过交接处时与轨道的碰撞所引起的能量损失可以不计, 取10m/s2)求:(1)滑块第1次经过光滑圆弧最低点B点时,轨道对滑块的支持力N的大小.
取10m/s2)求:(1)滑块第1次经过光滑圆弧最低点B点时,轨道对滑块的支持力N的大小.
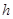 .
.