题目内容
（2011?南昌模拟）如图所示，真空中有直角坐标系xOy，P是坐标中的一个点，坐标是（a，-b）．有一质量为m、电荷量为+q的质点A从原点O沿y轴正方向以速度v0射出，不计重力的影响．（1）若在x≥0和y≥0的区域内加一个垂直于坐标系平面的匀强磁场，使质点A能通过P点．试求出磁感应强度B的大小和方向以及质点A从坐标原点O运动到P点的时间t；
（2）若在x轴上固定一个带负电的点电荷C，使质点A能保持速率不变，并通过P点．求点电荷C与坐标原点O的距离和点电荷C所带电荷量的大小，已知静电力常量为k．
分析：（1）质点进入匀强磁场后，受到洛伦兹力，做匀速圆周运动，画出轨迹，由几何知识求出半径，由牛顿第二定律求出磁感应强度B的大小．由左手定则判断B的方向．根据时间与周期的关系求出质点在磁场中运动的时间．质点进入第四象限后，做匀速直线运动，由位移与速度求出时间，再求总时间．
（2）洛伦兹力不做功，不能改变质点的速度大小．由题，使质点A能保持速率不变，质点应以点电荷C为圆心做匀速圆周运动，由几何知识求出半径．质点由库仑力提供向心力，根据牛顿第二定律求解点电荷C所带电荷量的大小．
（2）洛伦兹力不做功，不能改变质点的速度大小．由题，使质点A能保持速率不变，质点应以点电荷C为圆心做匀速圆周运动，由几何知识求出半径．质点由库仑力提供向心力，根据牛顿第二定律求解点电荷C所带电荷量的大小．
解答：解：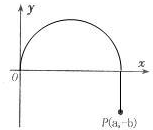
（1）在匀强磁场中，质点A做匀速圆周运动，半径R=
又有qv0B=m
，解得B=
，磁感应强度方向垂直纸面向外
在匀强磁场中的周期为T=
=
运动时间为t1=
=
质点A出匀速磁场后做匀速直线运动，运动时间为t2=
则总时间t=t1+t2=
（2）应以带电的点电荷C为圆心做匀速圆周运动，设半径为r，有
（a-r）2+b2=r2
解得，r=
故点电荷C与坐标原点O的距离为
．
又有k
=m
联立解得Q=
答：
（1）磁感应强度B=
，磁感应强度方向垂直纸面向外．质点A从坐标原点O运动到P点的时间t=
；
（2）点电荷C与坐标原点O的距离为
，点电荷C所带电荷量的大小Q=
．
（1）在匀强磁场中，质点A做匀速圆周运动，半径R=
| a |
| 2 |
又有qv0B=m
| ||
| R |
| 2mv0 |
| qa |
在匀强磁场中的周期为T=
| 2πm |
| qB |
| πa |
| v0 |
运动时间为t1=
| T |
| 2 |
| πa |
| 2v0 |
质点A出匀速磁场后做匀速直线运动，运动时间为t2=
| b |
| v0 |
则总时间t=t1+t2=
| πa+2b |
| 2v0 |
（2）应以带电的点电荷C为圆心做匀速圆周运动，设半径为r，有
（a-r）2+b2=r2
解得，r=
| a2+b2 |
| 2a |
故点电荷C与坐标原点O的距离为
| a2+b2 |
| 2a |
又有k
| r2 |
| ||
| r |
联立解得Q=
(a2+b2)m
| ||
| 2kaq |
答：
（1）磁感应强度B=
| 2mv0 |
| qa |
| πa+2b |
| 2v0 |
（2）点电荷C与坐标原点O的距离为
| a2+b2 |
| 2a |
(a2+b2)m
| ||
| 2kaq |
点评：本题是磁场中圆周运动与电场中圆周运动的比较，原理相同：分析受力，确定向心力的来源．根据几何知识求轨迹半径是关键．
练习册系列答案
相关题目
（2011?南昌模拟）如图a，质量m=1kg的物体沿倾角θ=37°的固定粗糙斜面由静止开始向下运动，风对物体的作用力沿水平方向向右，其大小与风速v成正比，比例系数用k表示，物体加速度a与风速v的关系如图b所示．（sin37°=0.6，cos37°=0.8，g=10m/s2）求：
（2011?南昌模拟）如图所示，两段长均为L的轻质线共同系住一个质量为m的小球，另一端分别固定在等高的A、B两点，A、B两点间距也为L，今使小球在竖直平面内做圆周运动，当小球到达最高点的速率为v时，两段线中张力恰好均为零，若小球到达最高点速率为2v，则此时每段线中张力为多少？（重力加速度为g）
（2011?南昌模拟）某兴趣小组在探究物体动能大小实验时，让一物体在恒定合外力作用下由静止开始沿直线运动，记录下速度、时间、位置等实验数据，然后分别作出动能EK随时间变化和动能EK随位置变化的两个图线，但横坐标没有标出，请你判断物体动能随位置变化的图线应是图