Question

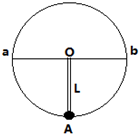
甲乙两小球质量相同，在光滑圆锥形漏斗的内壁做匀速圆周运动，如图所示，则有（　　）

A．ν甲＞ν乙

B．ω甲＞ω乙

C．a甲＞a乙

D．T甲＞T乙

Answer 1

为了分析计算的方便，我们把甲、乙两小球定义为A、B球．
对A、B两球进行受力分析，两球均只受重力和漏斗给的支持力F_N．如图所示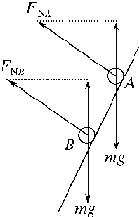
对A球由牛顿第二定律：
F_NAsinα=mg----------------------①
F_NAcosα=m

vA2

rA

=mω_A²r_{A-----------------------}②
对B球由牛顿第二定律：
F_NBsinα=mg----------------------③
F_NBcosα=m

vB2

rB

=mω_B²r_{B-------------------------}④
由两球质量相等可得F_NA=F_NB，所以C错误．
由②④可知，两球所受向心力相等．m

vA2

rA

=m

vB2

rB

，因为r_A＞r_B，所以v_A＞v_B，故A正确，B错误．
mω_A²r_A=mω_B²r_B，因为r_A＞r_B，所以ω_A＜ω_B，故又因为ω=

2π

T

，所以T_A＞T_B，故D正确．
故选：AD．