题目内容
18. 如图所示导体棒ab质量为100g,用绝缘细线悬挂.当悬线竖直时ab棒恰好与宽度为50cm的光滑水平导轨良好接触.导轨上放有质量为200g的另一导体棒cd,位置如图所示.整个装置处于竖直向上的磁感强度B=0.2T的匀强磁场中,现保持悬线伸直将ab棒拉起0.8m高后无初速释放.当ab第一次摆到最低点与导轨瞬间接触后,还能继续向左摆到0.45m高处,求:
如图所示导体棒ab质量为100g,用绝缘细线悬挂.当悬线竖直时ab棒恰好与宽度为50cm的光滑水平导轨良好接触.导轨上放有质量为200g的另一导体棒cd,位置如图所示.整个装置处于竖直向上的磁感强度B=0.2T的匀强磁场中,现保持悬线伸直将ab棒拉起0.8m高后无初速释放.当ab第一次摆到最低点与导轨瞬间接触后,还能继续向左摆到0.45m高处,求:(1)ab棒与导轨第一次接触前、后的速度大小.
(2)cd棒获得的速度大小;
(3)瞬间通过ab棒的电量;
(4)此过程中回路产生的焦耳热.
分析 (1)根据机械能守恒定律求出ab与导轨第一次接触前、后的速度大小.
(2)ab棒与导轨接触的过程,两棒组成系统所受安培力的合力为零,根据动量守恒定律求出cd棒获得的速度大小.
(3)根据动量定理求出瞬间通过ab棒的电量.
(4)根据能量守恒定律求出回路中产生的焦耳热.
解答 解:(1)ab棒下落过程中,切割磁感线,产生感应电动势,但没有感应电流,不受安培力,只有落到最低点时,接触导轨,与导轨cd棒组成闭合回路时才有感应电流产生.棒在向下、向上运动的过程中,只有重力做功,即机械能守恒.设ab棒与导轨第一次接触前、后的速度大小分别为v1和v2.
对ab棒,根据机械能守恒得:
下摆过程有:mgh1=$\frac{1}{2}m{v}_{1}^{2}$
得:v1=$\sqrt{2g{h}_{1}}$=$\sqrt{2×10×0.8}$=4m/s
上摆过程有:mgh2=$\frac{1}{2}m{v}_{2}^{2}$
得:v2=$\sqrt{2g{h}_{2}}$=$\sqrt{2×10×0.45}$=3m/s.
(2)当ab运动到最低点的瞬间,回路产生感应电流,磁场对ab、cd棒均有安培力作用,又因为系统在水平方向上合外力为零,即动量守恒.设cd棒获得的速度大小为v3,取向左为正方向,根据系统的动量守恒得:
m1v1=m1v2+m2v3
解得 v3=0.5m/s.
(3)对于ab棒,取向左为正方向,根据动量定理得:-FAt=mv2-mv1
则有 BILt=mv1-mv2,即:qBL=mv1-mv2
解得:q=$\frac{{m}_{1}({v}_{1}-{v}_{2})}{BL}$=$\frac{0.1×(4-3)}{0.2×0.5}$C=1C.
(4)根据能量守恒定律知,系统动能的减小量等于回路中产生的焦耳热.
Q=$\frac{1}{2}{m}_{1}{v}_{1}^{2}$-$\frac{1}{2}{m}_{1}{v}_{2}^{2}$-$\frac{1}{2}{m}_{2}{v}_{3}^{2}$=0.325J.
答:(1)ab棒与导轨第一次接触前、后的速度大小分别为4m/s和3m/s.
(2)cd棒获得的速度大小为0.5m/s.
(3)此瞬间通过ab棒的电量为1C.
(4)此过程回路产生的焦耳热为0.325J.
点评 本题综合考查了动量守恒定律、机械能守恒定律、动量定理、能量守恒定律等,综合性较强,关键要学会运用动量定理求电量.

 如图,正方形线圈边长为l,以速度v垂直且匀速穿过底边长为2l,高为2l的等腰三角形匀强磁场区域,若规定线圈abcd中的电流顺时针方向为正,下图中能正确表达电流随时间变化的图象是( )
如图,正方形线圈边长为l,以速度v垂直且匀速穿过底边长为2l,高为2l的等腰三角形匀强磁场区域,若规定线圈abcd中的电流顺时针方向为正,下图中能正确表达电流随时间变化的图象是( )| A. | 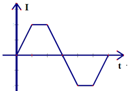 | B. |  | C. |  | D. |  |

| A. | 气体吸收热量,内能不变 | |
| B. | 气缸内分子的平均动能增大 | |
| C. | 单位时间内撞击气缸壁单位面积上的分子数增多 | |
| D. | 气缸内分子撞击气缸壁的平均作用力增大 |
 为研究钢球在液体中运动时所受到阻力的大小,让钢球从某一高度竖直落下进入液体中运动,用闪光照相方法拍摄钢球在不同时刻的位置,如图所示,已知钢球在液体中运动时所受阻力F=kv2,闪光照相机的闪光频率为f,图中刻度尺的最小分度为l0,钢球的质量为m,则阻力常数k的表达式为( )
为研究钢球在液体中运动时所受到阻力的大小,让钢球从某一高度竖直落下进入液体中运动,用闪光照相方法拍摄钢球在不同时刻的位置,如图所示,已知钢球在液体中运动时所受阻力F=kv2,闪光照相机的闪光频率为f,图中刻度尺的最小分度为l0,钢球的质量为m,则阻力常数k的表达式为( )| A. | $\frac{mg}{{l_0^2{f^2}}}$ | B. | $\frac{mg}{{2l_0^2{f^2}}}$ | C. | $\frac{mg}{{4l_0^2{f^2}}}$ | D. | $\frac{mg}{{8l_0^2{f^2}}}$ |
 如图所示电路可将声音信号转化为电信号,该电路中右侧固定不动的金属板b与能在声波驱动下沿水平方向振动的镀有金属层的振动膜a构成了一个电容器,a、b通过导线与恒定电源两极相接.若声源S做简谐运动,则( )
如图所示电路可将声音信号转化为电信号,该电路中右侧固定不动的金属板b与能在声波驱动下沿水平方向振动的镀有金属层的振动膜a构成了一个电容器,a、b通过导线与恒定电源两极相接.若声源S做简谐运动,则( )| A. | a振动过程中,a、b板之间的电场强度不变 | |
| B. | a振动过程中,a、b板所带的电荷量不变 | |
| C. | a振动过程中,灵敏电流计中始终有方向不变的电流 | |
| D. | a向右的位移最大时,a、b板构成的电容器的电容最大 |
 如图所示,完全相同的两球放在固定的斜面上,并用一竖直挡板MN挡住,两球的质量均
如图所示,完全相同的两球放在固定的斜面上,并用一竖直挡板MN挡住,两球的质量均为m,斜面的倾角为α,所有的摩擦均不计,则( )
| A. | 两球对斜面的压力大小均为mgcosα | B. | 斜面对B的弹力一定大于mg | ||
| C. | 挡板对B的弹力大小为2mgtanα | D. | B球对A球的弹力大小为$\frac{mg}{sinα}$ |
 一质量为1kg的物块置于水平地面上,现用一个水平恒力F拉物块,一段时间后撤去恒力F,已知从物块开始运动到停止,经历的时间为4s,运动的位移为10$\sqrt{3}$m,物块与地面间的动摩擦因数为$\frac{\sqrt{3}}{3}$(g=10m/s2).
一质量为1kg的物块置于水平地面上,现用一个水平恒力F拉物块,一段时间后撤去恒力F,已知从物块开始运动到停止,经历的时间为4s,运动的位移为10$\sqrt{3}$m,物块与地面间的动摩擦因数为$\frac{\sqrt{3}}{3}$(g=10m/s2). 如图所示,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力:
如图所示,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力: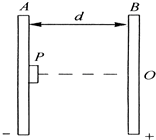 如图所示,在一个足够大的铅板A的右表面贴一放射源P.P可以向各个方向释放出β粒子,设速度大小v=107m/s,在A板右边相距d=2cm处放一平行于A的金属板B,使A带负电、B带正电后,板间形成场强大小为E=3.64×104N/C的匀强电场,试求β粒子打在B板上的范围.(β粒子的质量m=9.1×10-31kg,电量e=1.60×10-19C)
如图所示,在一个足够大的铅板A的右表面贴一放射源P.P可以向各个方向释放出β粒子,设速度大小v=107m/s,在A板右边相距d=2cm处放一平行于A的金属板B,使A带负电、B带正电后,板间形成场强大小为E=3.64×104N/C的匀强电场,试求β粒子打在B板上的范围.(β粒子的质量m=9.1×10-31kg,电量e=1.60×10-19C)