题目内容
【题目】如图甲所示,固定平行金属导轨MN、PQ与水平面成37°角倾斜放置,其电阻不计,相距为L=0.4 m.导轨顶端与电阻R相连,R=0.15 Ω.在导轨上垂直导轨水平放置一根质量为m=2×10-2 kg、电阻为r=0.05Ω的导体棒ab. ab距离导轨顶端d1=0.4 m,距离导轨底部d2=16 m,导体棒与导轨间的动摩擦因数μ=0.5;在装置所在区域加一个垂直导轨平面向上的磁场,其磁感应强度B和时间t的函数关系如图乙所示。(g取10 m/s2)
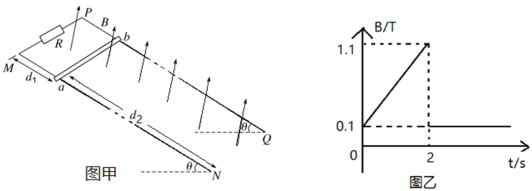
(1)前2s内,施加外力使导体棒保持静止,求通过导体棒的电流I的大小和方向
(2)前2s内,哪段时间内静止释放导体棒(不施加外力),释放时导体棒能处于平衡状态?
(3)若2s后静止释放导体棒,已知ab棒滑到底部前已达到最大速度vm并匀速下滑到底部。求vm的大小、以及此过程中电阻R上产生的热量Q和通过的电量q.
【答案】(1)0.4A,方向b→a(2)t=0.3~2.0 s时间段内释放导体棒时,导体棒处于平衡状态(3)5m/s;0.2925J;3.2C
【解析】
解:(1)设闭合回路产生的感应电动势为![]() ,则有:
,则有:![]()
代入数据可得:![]()
通过导体棒的电流的大小:![]() ,电流的方向从
,电流的方向从![]() 到
到![]()
(2)若导体棒即将向下运动,则有:![]()
代入数据得:![]()
若导体棒即将向上运动,则有:![]()
代入数据得:![]()
由图像得前两秒:![]()
代入![]() 、
、![]() 可得
可得![]() ,
,![]()
所以![]() 时间段内释放导体棒时,导体棒处于平衡状态
时间段内释放导体棒时,导体棒处于平衡状态
(3) 2s后释放导体棒,达到匀速时:![]()
![]()
代入数据得:![]()
下滑到底部过程中,由动能定理可得:![]()
代入数据得:![]()
此过程中电阻![]() 上产生的热量:
上产生的热量:![]()
通过的电量:![]()

练习册系列答案
相关题目