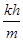Question

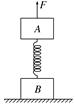
A、B两球质量分别为m₁与m₂，用一劲度系数为K的弹簧相连，一长为l₁的细线与m₁相连，置于水平光滑桌面上，细线的另一端拴在竖直轴OO`上，如图所示，当m<sub>1</sub>与m<sub>2</sub>均以角速度w绕OO`做匀速圆周运动时，弹簧长度为l₂。求：

（1）此时弹簧伸长量多大？绳子张力多大？
（2）将线突然烧断瞬间两球加速度各多大？

Answer 1

（1）  
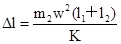
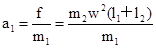
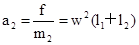
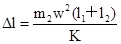
（2） 

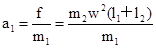
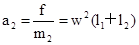
试题分析：（1）m₂只受弹簧弹力，设弹簧伸长Δl，满足
KΔl=m₂w²(l₁＋l₂)
∴弹簧伸长量
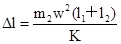
对m₁，受绳拉力T和弹簧弹力f做匀速圆周运动，
满足：T－f=m₁w²l₁
绳子拉力
（2）线烧断瞬间
A球加速度
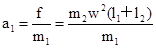
B球加速度
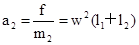
点评：本题考查了圆周运动向心力来源，并结合圆周运动知识建立等式求解。本题还考察了物体的惯性知识。