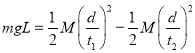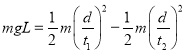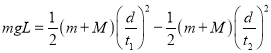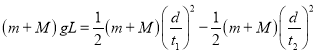题目内容
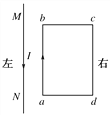
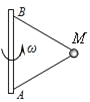
【题目】如图所示，物体M用两根长度相等不可伸长的线系在竖直杆上，它们随竖直杆转动，当转动角速度变化时，各力变化的情况为
A. ω只有超过某一数值时，绳AM的张力才出现
B. 绳BM的张力随ω的增大而增大
C. 不论ω如何变化，绳BM的张力总大于AM的张力
D. 当ω增大到某个值，总会出现AM的张力大于BM的张力的情况
【答案】ABC
【解析】
试题分析: 设BM绳与竖直方向的夹角为θ，AM绳与竖直方向的夹角为α，对物体M行受力分析，根据向心力公式则有：
①,
②;A、当ω较小时，BM绳在水平方向的分量可以提供向心力，此时AM绳没有力，当ω增加到某值时，BM绳在水平方向的分量不足以提供向心力，此时绳子AM才有力的作用，故A正确；B、ω的增大，所需的向心力增大，绳子BM和AM的力都增大，故B正确；C、D、当AM绳子没有拉直时，AM绳拉力等于零，BM绳肯定有拉力，当AM绳拉直时，θ=α，由①式可知，绳BM的张力一定大于绳子AM的张力，故C正确，D错误；故选ABC
练习册系列答案
小学教材完全解读系列答案
相关题目
