题目内容
【题目】如图1所示，AB段为一与水平面成37°角的光滑斜面，BCDE段为一传送带，BC段水平、角CDE也为37°，传送带与物体间动摩擦因数为0.5，转动轮大小不计．一弹簧一端固定在斜面的底端，另一端拴住质量为m1=4kg的小物块P，小物体Q与P接触，已知Q的质量为m2=10kg，弹簧的质量不计，劲度系数k=100N/m，系统恰好在斜面某位置处于静止，现给Q施加一个方向沿斜面向上的力F，使它们一起从静止开始沿斜面向上做匀加速运动，已知力F的大小随位移x按如图2所示规律变化 （sin 37°=0.6，cos37°=0.8，g=10m/s2） 求：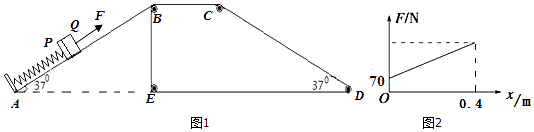
（1）刚开始时加力F时弹簧的压缩量
（2）求PQ一起运动的加速度的大小；如果PQ运动0.4m恰好到B点，求物体Q到B点时的速度大小
（3）如果运动0.4m到B点时，PQ刚好分离，同时撤去拉力F，传送带逆时针匀速转动，速度大小为10m/s，物体经过B点时利用特殊装置使使物体速度方向立即变为水平，大小不变，BC段距离为X=0.4m，当物体运动到C点时，传送带开始顺时针匀速转动，速度大小不变，CD段长度为S=22.25m，求物块从C运动到D所用时间．
【答案】
（1）解：静止状态下，PQ受力平衡，故设弹簧压缩量为x0，则有：kx0=（m1+m2）gsin37°=84N
解得：x0=0.84m；
答：刚开始时加力F时弹簧的压缩量为0.84m；
（2）解：PQ一起运动，位移为x时，弹簧弹力为k（x0﹣x），故当P、Q开始运动时拉力最小，由牛顿第二定律可得：Fmin=（m1+m2）a
解得： 
；
那么，由匀变速运动规律可得：物体Q到B点时的速度大小为： 
；
答：PQ一起运动的加速度的大小为5m/s2；如果PQ运动0.4m恰好到B点，那么物体Q到B点时的速度大小为2m/s；
（3）解：在水平传送带BC上，物体（记质量为m）受到向左的摩擦力f=μmg，那么物体在BC上运动只有摩擦力做功，故由动能定理可得： 
代入数据解得：vC=0；
物体在CD上运动，当物体速度小于传送带速度时，合外力为：F1=mgsin37°+μmgcos37°=mg
那么物体运动加速度为： 
；
故物体要达到传送带速度需要运动位移为： 
运动时间为： 
；
之后物体合外力为：F2=mgsin37°﹣μmgcos37°=0.2mg
故物体做加速度为 
的匀加速直线运动，那么有： 
代入数据解得：t2=1.5s；
故物块从C运动到D所用时间为：t=t1+t2=2.5s；
答：如果运动0.4m到B点时，PQ刚好分离，同时撤去拉力F，传送带逆时针匀速转动，速度大小为10m/s，物体经过B点时利用特殊装置使使物体速度方向立即变为水平，大小不变，BC段距离为X=0.4m，当物体运动到C点时，传送带开始顺时针匀速转动，速度大小不变，CD段长度为S=22.25m，则物块从C运动到D所用时间为2.5s．
【解析】（1）根据受力平衡条件进行求解。
（2）根据牛顿第二运动定律结合运动学公式进行求解。
（3）传送带上物体的运动情况要根据受力情况结合计算进行判断，对小物体进行受力分析，开始小物体能沿传送带向上做匀加速直线运动．根据动能定理列式进行计算。
【考点精析】根据题目的已知条件，利用匀变速直线运动的速度、位移、时间的关系和动能定理的综合应用的相关知识可以得到问题的答案，需要掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值；应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
