题目内容
如图所示，在水平桌面上做匀速运动的两个小球，质量分别为m1和m2，沿着同一直线向相同的方向运动，速度分别为V1和V2，当第二个小球追上第一个小球时两球相碰，碰后的速度分别为V1′和V2′，试根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和．
证明：根据牛顿第二定律，碰撞过程中两球的加速度分别是：
a1=
a2=
根据牛顿第三定律F1与F2大小相等，方向相反，即：
F1=-F2
所以有：m1a1=-m2a2
碰撞时两球之间力的作用时间很短，用△t表示．这样，加速度与碰撞前后速度的关系就是：
a1=
a2=
把加速度的表达式代人 m1a1=-m2a2移项后得到：
m1v1+m2v2=m1v′1+m2v′2
即可证：两球碰撞前的动量之和等于碰撞后的动量之和．
答：根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和见上．
a1=
| F1 |
| m1 |
| F2 |
| m2 |
根据牛顿第三定律F1与F2大小相等，方向相反，即：
F1=-F2
所以有：m1a1=-m2a2
碰撞时两球之间力的作用时间很短，用△t表示．这样，加速度与碰撞前后速度的关系就是：
a1=
| v′1-v1 |
| △t |
| v′2-v2 |
| △t |
把加速度的表达式代人 m1a1=-m2a2移项后得到：
m1v1+m2v2=m1v′1+m2v′2
即可证：两球碰撞前的动量之和等于碰撞后的动量之和．
答：根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和见上．
练习册系列答案
相关题目
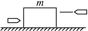
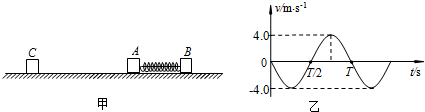时，物体A的速度?时间图象如图乙所示．求：
