题目内容
12.在公交车行驶中,司机能从车旁边的后视镜内看到车后离车头L=20米范围以内的物体,若该客车由静止开始以a=1.0m/s2的加速度做匀加速直线运动,与此同时,在距车头x=32米远的地方有一乘客正以v=5m/s匀速追赶该客车,在追赶过程中只有乘客在后视镜内的像持续保留时间不少于1.8s时,司机才能留意到该乘客而停车并等待乘客上车,则从客车由静止启动开始计时:(1)经过多长时间司机第一次能看到该乘客?
(2)经过多长时间乘客距离客车最近?最近距离为多少?
(3)乘客能成功登上客车吗?请说明理由.
分析 (1)根据位移关系,结合运动学公式求出第一次看到乘客的时间.
(2)当人和车的速度相等时,相距最近,结合运动学公式求出最近距离.
(3)根据两两者距离在20m范围内的时间差,判断乘客能否成功登车.
解答 解:(1)根据$vt-\frac{1}{2}a{t}^{2}=x-L$得,$5t-\frac{1}{2}×1×{t}^{2}=12$.
解得t1=4s,t2=6s.
可知经过4s司机第一次看到乘客.
(2)当汽车和人的速度相等时,相距最近,
t=$\frac{v}{a}=\frac{5}{1}s=5s$,
最近距离$△x=\frac{1}{2}a{t}^{2}+x-vt=\frac{1}{2}×1×25+32-5×5$m=19.5m.
(3)根据△t=t2-t1=6-4s=2s>1.8s,可知司机会发现乘客,则乘客能成功登车.
答:(1)经过4s时间司机第一次看到乘客.
(2)经过5s时间乘客距离客车最近,最近距离为19.5m,
(3)乘客能成功登车,因为在追赶过程中只有乘客在后视镜内的像持续保留时间不少于1.8s.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时,有最近距离.

练习册系列答案
相关题目
3.关于重力和重心的说法正确的是( )
| A. | 物体的重心一定在物体上 | |
| B. | 重力的大小可以用天平直接测量 | |
| C. | 重力的方向总是垂直向下 | |
| D. | 重力是由于地球的吸引而使物体受到的力 |
20.下列说法中不正确的是( )
| A. | 根据速度定义式v=$\frac{△x}{△t}$,当△t极小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了极限的思想方法 | |
| B. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一段近似看成匀速直线运动,然后把各小段的位移相加,这里运用了控制变量法 | |
| C. | 物体在某段时间内的平均速度越大,在其间任一时刻的瞬时速度也一定越大 | |
| D. | 意大利科学家伽利略在研究运动和力的关系时,提出了著名的斜面实验运用了理想实验的方法 |
2. 如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根弹性轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )
如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根弹性轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )
 如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根弹性轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )
如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根弹性轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是( )| A. | 斜面受地面的摩擦力向右 | |
| B. | 地面对斜面的支持力为82N | |
| C. | 球对弹性轻杆的作用力为2N,方向竖直向下 | |
| D. | 弹性轻杆对小球的作用力为2N,方向垂直斜面向上 |
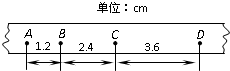 在研究匀变速直线运动规律的实验中,如图所示为一次记录小车运动情况的纸带.图中A、B、C、D为相邻的计数点,相邻计数点的时间间隔为T=0.1秒,则:
在研究匀变速直线运动规律的实验中,如图所示为一次记录小车运动情况的纸带.图中A、B、C、D为相邻的计数点,相邻计数点的时间间隔为T=0.1秒,则: 如图所示,一半径为R,位于竖直面内的绝缘光滑轨道上静止着两个相同的带电小球A和B(可视为质点),两球质量均为m,距离为R,用外力慢慢推左球A使其到达圆周最低点C.求此过程中外力所做的功.
如图所示,一半径为R,位于竖直面内的绝缘光滑轨道上静止着两个相同的带电小球A和B(可视为质点),两球质量均为m,距离为R,用外力慢慢推左球A使其到达圆周最低点C.求此过程中外力所做的功. 如图所示,A、B为平行金属板,两板相距为d,分别与电源两极相连,两板的中央各有一小孔M和N,今有一带电粒子m,带电量q,自A板上方相距为h的P点由静止自由下落(P、M、N在同一竖直线上),空气阻力忽略不计,到达N孔时速度恰好为零,若保持两极板间电压不变,取g=10m/s2.求:
如图所示,A、B为平行金属板,两板相距为d,分别与电源两极相连,两板的中央各有一小孔M和N,今有一带电粒子m,带电量q,自A板上方相距为h的P点由静止自由下落(P、M、N在同一竖直线上),空气阻力忽略不计,到达N孔时速度恰好为零,若保持两极板间电压不变,取g=10m/s2.求: