��Ŀ����
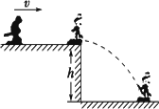
����Ŀ����ͼ��ʾΪij�����Ϸʾ��ͼ���⻬ˮƽ̨���Ϲ̶�����������ֱ�⻬Բ������ֲ�б��AB����ֱ��BC����ֱ�а�MN��ͨ���������˽��������ĵ���ѹ��һ��������ͷ�,�����O�㵯������E�����Բ���,��תһ�ܺ������ƽֱ�����ǰ��,��A����б��AB�����˶�,�����B������а�Ŀ��(�����ˮƽ�滬��б��ʱ����������ʧ)����֪��������m=0.05kg��б�������=37����б�泤L=2.5m��������б��AB֮��Ķ�Ħ��������=0.5����ֱ��BC��а�MN�����Ϊd��B����а���10�����ĵ�P����ֱ����![]() �����Կ�������,�������Ϊ�ʵ㡣��֪
�����Կ�������,�������Ϊ�ʵ㡣��֪![]() ,ȡ
,ȡ![]() ����:
����:

(1)��Ҫʹ����ǡ���ܹ�����B�㣬��Բ������������뾶Ϊ���?
(2)����һ�ε����з��ֻ���ǡ��ˮƽ���аа��ϵ�P�㣬��˴λ��鱻����ǰ���ɱ�ѹ�������ʱ�ĵ�������Ϊ���?
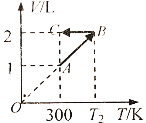
(3)��MN�����ˮƽ���������ƶ�������Զ��б�棬�Ա�֤�����B���������ˮƽ���аа塣��B��Ϊ����ԭ�㣬����ˮƽ��ֱ����ϵ(��ͼ)����ˮƽ���аа�λ������(x��y)Ӧ����ʲô����?
���𰸡���1m����1.875J����![]()
��������
(1)��Բ��������İ뾶���ֵΪR����Բ�����ߵ㣺
![]()
Ҫʹ����ǡ���ܵ���B�㣬����
![]()
��Բ�����ߵ���B��Ĺ��̣�
![]()
�������ݿɵ�
![]()
(2)����ǡ��ˮƽ���аа��ϵ�P�㣬B��P�˶��������Ϊƽ���˶�
��B��P��
![]()
![]()
![]()
�������ݿɵã�
![]()
�ӵ�������B�Ĺ��̣�
![]()
�������ݿɵã�
![]()
(3)ͬ������ƽ���ɵ����ۿ�֪��
![]()
��
![]() ��
��
��![]() ����
����![]()