题目内容
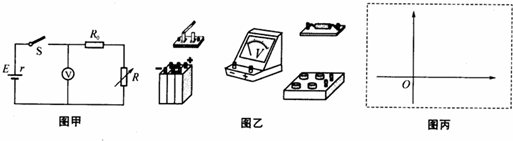
（2009?江苏模拟）如图（A）所示，固定于水平桌面上的金属架cdef，处在一竖直向下的匀强磁场中，磁感强度的大小为B
0，金属棒ab搁在框架上，可无摩擦地滑动，此时adeb构成一个边长为l的正方形，金属棒的电阻为r，其余部分的电阻不计．从t=0的时刻起，磁场开始均匀增加，磁感强度变化率的大小为k（k=
）．求：
（1）用垂直于金属棒的水平拉力F使金属棒保持静止，写出F的大小随时间 t变化的关系式．
（2）如果竖直向下的磁场是非均匀增大的（即k不是常数），金属棒以速度v
0向什么方向匀速运动时，可使金属棒中始终不产生感应电流，写出该磁感强度B
t随时间t变化的关系式．
（3）如果非均匀变化磁场在0-t
1时间内的方向竖直向下，在t
1-t
2时间内的方向竖直向上，若t=0时刻和t
1时刻磁感强度的大小均为B
0，且adeb的面积均为l
2．当金属棒按图（B）中的规律运动时，为使金属棒中始终不产生感应电流，请在图（C）中示意地画出变化的磁场的磁感强度B
t随时间变化的图象（t
1-t
0=t
2-t
1＜
）．
分析：（1）根据法拉第电磁感应定律求出感应电动势的大小，结合闭合电路欧姆定律求出感应电流的大小，抓住外力F与安培力相等求出外力F与时间的关系式．
（2）要使金属棒中不产生感应电流，抓住回路中的磁通量变化量为零，求出磁感应强度随时间的变化的关系式．
（3）抓住磁通量变化量为零，得出磁感应强度的表达式，从而得出磁感应强度随t的变化图象．
解答：
解：（1）ε=
=
S=kl
2 I=
=
因为金属棒始终静止，在t时刻磁场的磁感强度为B
t=B
0+kt，所以
F
外=F
A=BIl=（ B
0+kt ）
l=B
0 +
t 方向向右
（2）根据感应电流产生的条件，为使回路中不产生感应电流，回路中磁通量的变化应为零，
因为磁感强度是逐渐增大的，所以金属棒应向左运动（使磁通量减小）
即：△φ=0，即△φ=B
tS
t-B
0S
0，
也就是 B
t l（l-vt ）=B
0l
2 得 B
t=
（3）如果金属棒的右匀速运动，因为这时磁感强度
是逐渐减小的，同理可推得，
B
t=
．
所以磁感强度随时间变化的图象如右图（t
2时刻B
t不为零）
答：（1）F的大小随时间 t变化的关系式为B
0 +
t．
（2）磁感强度B
t随时间t变化的关系式 B
t=
．
（3）如图所示．
点评：本题根据法拉第电磁感应定律求解感应电动势，由欧姆定律和安培力公式推导安培力的表达式，是常用的方法和思路．当回路中没有感应电流产生时，回路总的磁通量应保持不变．
练习册系列答案
相关题目
名校课堂系列答案
（2009?江苏模拟）实验室经常使用的电流表是磁电式仪表．这种电流表的构造如图甲所示．蹄形磁铁和铁芯间的磁场是均匀地辐向分布的．当线圈通以如图乙所示的电流，下列说法正确的是（ ）
（2009?江苏模拟）如图所示，质量分别为m1、m2的两个物块间用一轻弹簧连接，放在倾角为θ的粗糙斜面上，物块与斜面间的动摩擦因数均为μ．平行于斜面、大小为F的拉力作用在m1上，使m1、m2一起向上作匀加速运动，斜面始终静止在水平地面上，则（ ）