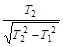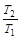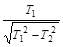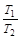Question

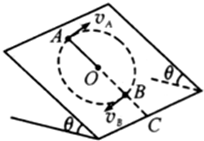
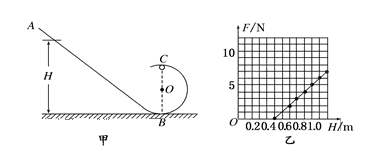
如图，木板A静止在光滑水平面上，其左端与固定台阶相距x，与滑块B（可视为质点）相连的细线一端固定在O点，水平拉直细线时滑块由静止释放，当B到达最低点时，细线断开，B恰好从A右端上表面水平滑入。A与台阶碰撞无机械能损失，不计空气阻力。已知A的质量为2m，B的质量为m，A、B之间动摩擦因数为μ=0.3，细线长为L=0.45m；且A足够长，B不会从A脱离；重力加速度为g=10m/s²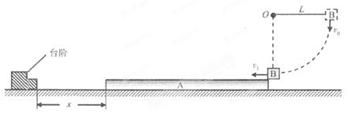

（1）求细线被拉断瞬间B的速度大小v₁
（2）A与台阶发生碰撞前瞬间，A、B刚好共速，求x为多少？
（3）在满足（2）条件下，A与台阶碰撞后最终的速度为多少？

Answer 1

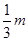（1）3m/s (2) （3）

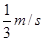
解析试题分析：（1）滑块B到达最低点的速度为v_1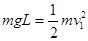
,解得v₁=3m/s
(2)A与B共速的速度为v₂,则 mv₁=3mv₂ ,v₂=1m/s
A在B上滑动过程中，对物体A由 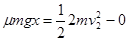，解得x=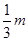
（3）A与台阶碰撞后,A将以原速率反弹，而B则以原来速度向左滑动，两者最终速度为v,由动量守恒定律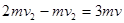
，解得v=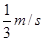
考点：机械能守恒定律、动量守恒定律及能量守恒定律。