题目内容
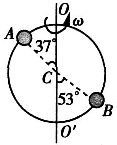
圆环绕通过直径的竖直轴OO'匀速转动,在圆环上套有两个质量相等的小球,如图所示,连接小球与圆环中心C的连线AC、BC分别与转轴成37°和53°角,转动中小球均没有在圆环上滑动.已知sin37°=0.6,sin53°=0.8.下列说法中错误的是( )
A.圆环对A的弹力方向可能沿AC方向向下
B.圆环对B的弹力方向只能沿BC方向向上
C.A与圆环间可能没有摩擦力
D.A、B两球所受的合力大小之比为3:4
【答案】分析:可以假设两种极限情况:1、转速很小,缓慢转动,近似平衡状态;2、假设转速很大,都有离心趋势.
解答:解:A、假设转速很大,A球有离心趋势,球内侧靠近圆心的一侧与圆环间相互挤压,圆环对A的弹力方向沿AC方向向下,故A正确;
B、转速较小时,圆球有下滑趋势,支持力指向圆心;转速很大时,有离心趋势,支持力仍然指向圆心;故B正确;
C、若A与圆环间没有摩擦力,A球受重力和支持力,合力不可能垂直指向OO′轴,故C错误;
D、A、B两球同轴转动,角速度相等,合力提供向心力,转动半径之比为Rsin37°:Rsin53°=3:4,根据向心力公式F=mω2r,合力之比为3:4,故D正确;
本题选错误的,故选C.
点评:本题难点在于弹力方向的判断,可以采用极值法,分角速度很小和很大两种极值情况判断.
解答:解:A、假设转速很大,A球有离心趋势,球内侧靠近圆心的一侧与圆环间相互挤压,圆环对A的弹力方向沿AC方向向下,故A正确;
B、转速较小时,圆球有下滑趋势,支持力指向圆心;转速很大时,有离心趋势,支持力仍然指向圆心;故B正确;
C、若A与圆环间没有摩擦力,A球受重力和支持力,合力不可能垂直指向OO′轴,故C错误;
D、A、B两球同轴转动,角速度相等,合力提供向心力,转动半径之比为Rsin37°:Rsin53°=3:4,根据向心力公式F=mω2r,合力之比为3:4,故D正确;
本题选错误的,故选C.
点评:本题难点在于弹力方向的判断,可以采用极值法,分角速度很小和很大两种极值情况判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 圆环绕通过直径的竖直轴OO'匀速转动,在圆环上套有两个质量相等的小球,如图所示,连接小球与圆环中心C的连线AC、BC分别与转轴成37°和53°角,转动中小球均没有在圆环上滑动.已知sin37°=0.6,sin53°=0.8.下列说法中错误的是( )
圆环绕通过直径的竖直轴OO'匀速转动,在圆环上套有两个质量相等的小球,如图所示,连接小球与圆环中心C的连线AC、BC分别与转轴成37°和53°角,转动中小球均没有在圆环上滑动.已知sin37°=0.6,sin53°=0.8.下列说法中错误的是( )