题目内容
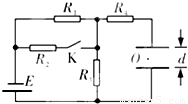
 如图所示的电路中,4个电阻的阻值均为R,E为直流电源电动势,其内阻可以不计,平行板电容器两极板间的距离为d.在平行极板电容器的两个平行极板之间有一个质量为m的带电小球.当电键K闭合时,带电小球静止在两极板间的中点O上.
如图所示的电路中,4个电阻的阻值均为R,E为直流电源电动势,其内阻可以不计,平行板电容器两极板间的距离为d.在平行极板电容器的两个平行极板之间有一个质量为m的带电小球.当电键K闭合时,带电小球静止在两极板间的中点O上.(1)求小球所带的电荷的极性和电量
(2)现把电键打开,带电小球便往平行极板电容器的某个极板运动,并与此极板碰撞,设在碰撞时没有机械能损失,但带电小球的电荷量发生变化.碰后小球带有与该极板相同性质的电荷,而且所带的电荷量恰好刚能使它运动到平行极板电容器的另一极板.求小球与电容器某个极板碰撞后所带的电荷量.
分析:(1)先分析等效电路,明确电容器极板间的电压与R3的电压相同,然后根据受力平衡状态确定小球受的电场力大小以及电性,从而计算其所带的电荷量;
(2)小球向下运动过程根据动能定理列一个方程,再根据碰撞后的运动情况列一个动能定理方程求解
(2)小球向下运动过程根据动能定理列一个方程,再根据碰撞后的运动情况列一个动能定理方程求解
解答:解:由电路图看以看出,因 R4之路上无电流,电容器两极板间电压,无论K是否闭合始终等于R3 上的电压,当K闭合时,设此两极板间电压为U,电源电动势为E,由分压关系可得
U=U3=
E ①
小球处于静止状态,由平衡条件得:
所以 q=
带正电
(2)当K断开时,由 R1和 R3串联可得电容两极板间电压为U′=
③
由①③两式得:U′=
E ④
U′<U表明K断开后小球将向下运动,重力对小球做正功,电场力对小球做负功,由功能关系可知:
mg
-q
=
mv2-0 ⑤
因小球与下极板碰撞时无机械能损失,设小球碰后电荷量变为q′,由功能关系得:
q′u′-mgd=0-
mv2 ⑥
联立上述各式解得:q′=
即小球与下极板碰后电荷符号不变,电荷量变为q′=
答:(1)小球所带的电荷的极性为正,电量为
(2)小球与极板碰后电荷量为得
.
U=U3=
| 2 |
| 3 |
小球处于静止状态,由平衡条件得:
所以 q=
| 3mgd |
| 2E |
(2)当K断开时,由 R1和 R3串联可得电容两极板间电压为U′=
| E |
| 2 |
由①③两式得:U′=
| 3 |
| 4 |
U′<U表明K断开后小球将向下运动,重力对小球做正功,电场力对小球做负功,由功能关系可知:
mg
| d |
| 2 |
| U′ |
| 2 |
| 1 |
| 2 |
因小球与下极板碰撞时无机械能损失,设小球碰后电荷量变为q′,由功能关系得:
q′u′-mgd=0-
| 1 |
| 2 |
联立上述各式解得:q′=
| 7mgd |
| 4E |
即小球与下极板碰后电荷符号不变,电荷量变为q′=
| 7mgd |
| 4E |
答:(1)小球所带的电荷的极性为正,电量为
| 3mgd |
| 2E |
(2)小球与极板碰后电荷量为得
| 7mgd |
| 4E |
点评:本题的关键是知道与电容器串联的电阻都相当于导线,电阻忽略不计,然后根据受力平衡以及动能定理求解即可.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目