题目内容
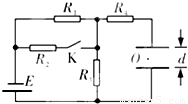
(13分)如图所示的电路中,4个电阻的阻值均为R,E为直流电源电动势,其内阻可以不计,平行板电容器两极板间的距离为d.在平行极板电容器的两个平行极板之间有一个质量为m的带电小球.当电键K闭合时,带电小球静止在两极板间的中点O上.

(1)求小球所带的电荷的极性和电量
(2)现把电键打开,带电小球便往平行极板电容器的某个极板运动,并与此极板碰撞,设在碰撞时没有机械能损失,但带电小球的电荷量发生变化.碰后小球带有与该极板相同性质的电荷,而且所带的电荷量恰好刚能使它运动到平行极板电容器的另一极板.求小球与电容器某个极板碰撞后所带的电荷量.
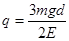 ,带正电(2)
,带正电(2)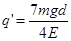
【解析】由电路图可以看出,因R4支路上无电流,电容器两极板间电压,无论K是否闭合始终等于电阻R3上的电压U3,当K闭合时,设此两极板间电压为U,电源的电动势为E,由分压关系可得U=U3=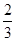 E ① (2分)
E ① (2分)
小球处于静止,由平衡条件得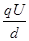 =mg ②
(1分)
=mg ②
(1分)
所以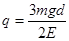 ,带正电
(2分)
,带正电
(2分)
(2)当K断开,由R1和R3串联可得电容两极板间电压为U′=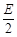 ③(1分)
③(1分)
由①③式得U′=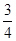 U ④(1分)
U ④(1分)
U′<U表明K断开后小球将向下极板运动,重力对小球做正功,电场力对小球做负功,由功能关系可知
mg =
= mv2-0 ⑤(2分)
mv2-0 ⑤(2分)
因小球与下极板碰撞时无机械能损失,设小球碰后电荷量变为q′,由功能关系得
q′U′-mgd=0- mv2 ⑥(2分)
mv2 ⑥(2分)
联立上述各式解得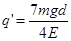 (1分)
(1分)
即小球与下极板碰后电荷符号未变,电荷量变为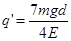 (1分)
(1分)
本题考查含容电路的分析,由电路图可以看出,因R4支路上无电流,电容器两极板间电压,无论K是否闭合始终等于电阻R3上的电压U3,当K闭合时,设此两极板间电压为U,电源的电动势为E,由分压关系可得U=U3=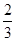 E,再以小球为研究对象,当小球静止时所受重力与电场力平衡,由此可求得小球电荷量大小和电性,当K断开后,由串联分压可求得电容器两端电压,同理求得电场力,再由动能定理可求得电场力做功,从而求得电荷电量
E,再以小球为研究对象,当小球静止时所受重力与电场力平衡,由此可求得小球电荷量大小和电性,当K断开后,由串联分压可求得电容器两端电压,同理求得电场力,再由动能定理可求得电场力做功,从而求得电荷电量

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 如图所示的电路中,4个电阻的阻值均为R,E为直流电源电动势,其内阻可以不计,平行板电容器两极板间的距离为d.在平行极板电容器的两个平行极板之间有一个质量为m的带电小球.当电键K闭合时,带电小球静止在两极板间的中点O上.
如图所示的电路中,4个电阻的阻值均为R,E为直流电源电动势,其内阻可以不计,平行板电容器两极板间的距离为d.在平行极板电容器的两个平行极板之间有一个质量为m的带电小球.当电键K闭合时,带电小球静止在两极板间的中点O上.