题目内容
 如图,长木板ab的b端固定一档板,木板连同档板的质量为M=4kg,ab间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=5.0m/s沿木板向前滑动,直到和档板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
如图,长木板ab的b端固定一档板,木板连同档板的质量为M=4kg,ab间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=5.0m/s沿木板向前滑动,直到和档板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.分析:由于木板和小物块所受外力之和为零,则可知动量守恒,由动量守恒定律可求得最后共同的速度;由功能关系可得出损失的总机械能,而机械能的损失来自于碰撞与摩擦力做功,则求出摩擦力所做的功即可求得碰撞中损失的机械能.
解答:解:全过程由动量守恒定律可得:mυ0=(M+m)υ,
解得:υ=
=1m/s,
全过程产生的焦耳热由相对位移可得:Q=μmg?2s=4J,
由能量守恒定律可得:
m
=
(M+m)υ2+Q+W损
解得:W损=6J;
答:碰撞过程中损失的机械能为6J.
解得:υ=
| mυ0 |
| M+m |
全过程产生的焦耳热由相对位移可得:Q=μmg?2s=4J,
由能量守恒定律可得:
| 1 |
| 2 |
| υ | 2 0 |
| 1 |
| 2 |
解得:W损=6J;
答:碰撞过程中损失的机械能为6J.
点评:本题考查动量守恒及功能关系,应明确机械能的损失有两部分,一部分来自于碰撞,另一部分来自于摩擦力做功,而本题只求碰撞所损失的机械能.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
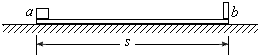 (2007?黑龙江一模)如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
(2007?黑龙江一模)如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能. 如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2
如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2
