题目内容
 如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2
如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2(1)碰撞后,若小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
(2)若s=1.5m,碰撞过程中损失的机械能为3.0J,求长木板的最终速度大小?
分析:(1)木板和小物块组成的系统所受合外力为零,在整个过程中,系统动量动量守恒,由动量守恒定律可求得最后共同的速度;由能量守恒定律可以求出损失的机械能,机械能的损失来自于碰撞与摩擦力做功,则求出摩擦力所做的功即可求得碰撞中损失的机械能.
(2)物块与挡板碰撞过程中要损失机械能,物块与木板间相对滑动克服摩擦力做功转化为系统内能机械能有损失,由能量守恒定律可以求出系统损失的机械能;物块与木板组成的系统在整个过程中所受合外力为零,系统动量守恒,由动量守恒定律可以求出木板的最终速度.
(2)物块与挡板碰撞过程中要损失机械能,物块与木板间相对滑动克服摩擦力做功转化为系统内能机械能有损失,由能量守恒定律可以求出系统损失的机械能;物块与木板组成的系统在整个过程中所受合外力为零,系统动量守恒,由动量守恒定律可以求出木板的最终速度.
解答:解:(1)设木板和物块最后共同运动的速度为v,设全过程损失的机械能为E,
由动量守恒定律mv0=(m+M)v…①
由能量守恒定律得:E=
mv02-
(m+M)v2…②,
用W表示在全过程中摩擦力做的总功,则W=-2μmgs…③
用E1表示在碰撞过程中损失的机械能,则E1=E-W…④
由以上各式解得:E=
v02-2μmgs…⑤
代入数据解锝:E1=2.4J;
(2)小物块恰好回到a端而不脱离木板,
则克服摩擦力做功转化为系统内能而损失的机械能:
Q=2μmgs′=2×0.1×1×10×1.5=3J,
则系统损失的总机械能E总=Q+E碰撞=3+3=6J,
系统最终的总机械能:EK=
mv02-E总=
×1×42-6=2J,
系统最终的总机械能:EK=
mv物块2+
Mv木板2
=
×1×v物块2+
×4×v木板2=2,
即:v物块2+4v木板2=4…⑥
物块与木板组成的系统动量守恒,
由动量守恒定律得:mv0=mv物块+Mv木板,
即:1×4=1×v物块+4×v木板,4=v物块+4v木板 …⑦
由⑥⑦解得:v木板=1m/s;
答:(1)碰撞过程中损失的机械能为2.4J.
(2)长木板的最终速度为1m/s.
由动量守恒定律mv0=(m+M)v…①
由能量守恒定律得:E=
| 1 |
| 2 |
| 1 |
| 2 |
用W表示在全过程中摩擦力做的总功,则W=-2μmgs…③
用E1表示在碰撞过程中损失的机械能,则E1=E-W…④
由以上各式解得:E=
| mM |
| 2(m+M) |
代入数据解锝:E1=2.4J;
(2)小物块恰好回到a端而不脱离木板,
则克服摩擦力做功转化为系统内能而损失的机械能:
Q=2μmgs′=2×0.1×1×10×1.5=3J,
则系统损失的总机械能E总=Q+E碰撞=3+3=6J,
系统最终的总机械能:EK=
| 1 |
| 2 |
| 1 |
| 2 |
系统最终的总机械能:EK=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
即:v物块2+4v木板2=4…⑥
物块与木板组成的系统动量守恒,
由动量守恒定律得:mv0=mv物块+Mv木板,
即:1×4=1×v物块+4×v木板,4=v物块+4v木板 …⑦
由⑥⑦解得:v木板=1m/s;
答:(1)碰撞过程中损失的机械能为2.4J.
(2)长木板的最终速度为1m/s.
点评:本题考查动量守恒及功能关系,应明确机械能的损失有两部分,一部分来自于碰撞,另一部分来自于摩擦力做功,而本题只求碰撞所损失的机械能.

练习册系列答案
相关题目
 如图,长木板ab的b端固定一档板,木板连同档板的质量为M=4kg,ab间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=5.0m/s沿木板向前滑动,直到和档板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
如图,长木板ab的b端固定一档板,木板连同档板的质量为M=4kg,ab间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=5.0m/s沿木板向前滑动,直到和档板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.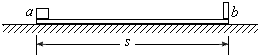 (2007?黑龙江一模)如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
(2007?黑龙江一模)如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
