题目内容
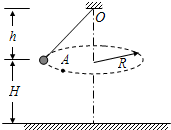 (2007?广州模拟)如图所示,用细线吊着一个小球,使小球在水平面内做半径为R的匀速圆周运动;圆周运动的水平面与悬点的距离为h,与水平地面的距离为H.若细线突在A处断裂,求小球在地面上的落点P与A的水平距离.
(2007?广州模拟)如图所示,用细线吊着一个小球,使小球在水平面内做半径为R的匀速圆周运动;圆周运动的水平面与悬点的距离为h,与水平地面的距离为H.若细线突在A处断裂,求小球在地面上的落点P与A的水平距离.分析:小球重力和拉力的合力提供圆周运动的向心力,根据牛顿第二定律求出细线断裂时的速度,根据平抛运动的知识求出小球在地面上的落点P与A的水平距离.
解答:解:设细线与竖直方向上的夹角为θ,根据牛顿第二定律得,mgtanθ=m
又tanθ=
则v=R
.
由H=
gt2,t=
.
则x=vt=R
?
=R
.
答:小球在地面上的落点P与A的水平距离为R
.
| v2 |
| R |
又tanθ=
| R |
| h |
则v=R
|
由H=
| 1 |
| 2 |
|
则x=vt=R
|
|
| 2Hh |
答:小球在地面上的落点P与A的水平距离为R
| 2Hh |
点评:本题综合考查了平抛运动和圆周运动,关键掌握平抛运动在水平方向和竖直方向上运动规律以及圆周运动向心力的来源.

练习册系列答案
相关题目
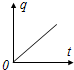 (2007?广州模拟)一个阻值为R的电阻两端加上电压U后,通过导体截面的电量q与通电时间t的图象如图所示,此图线的斜率(即tanα)等于( )
(2007?广州模拟)一个阻值为R的电阻两端加上电压U后,通过导体截面的电量q与通电时间t的图象如图所示,此图线的斜率(即tanα)等于( ) (2007?广州模拟)如图所示,有一混合正离子束先后通过正交电磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径R相同,则它们具有相同的( )
(2007?广州模拟)如图所示,有一混合正离子束先后通过正交电磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径R相同,则它们具有相同的( ) (2007?广州模拟)如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( )
(2007?广州模拟)如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( ) (2007?广州模拟)如图所示表示作用在某物体上的合外力随时间变化的关系,若物体开始时是静止的,则前3s内( )
(2007?广州模拟)如图所示表示作用在某物体上的合外力随时间变化的关系,若物体开始时是静止的,则前3s内( )