题目内容
 (2007?广州模拟)如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( )
(2007?广州模拟)如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( )分析:重物在水平面上做匀速圆周运动时,绳子的拉力提供向心力,根据牛顿第二定律,向心力分别用转速、周期、线速度表示,研究拉力与它们的关系,分析求解.
解答:解:A、根据牛顿第二定律得:F=m(2πn)2r,m一定,当转速n相同时,绳长r越长,绳子拉力F越大,绳子越容易断.故A正确.
B、根据牛顿第二定律得:F=m
,m一定,当周期T相同时,绳长r越长,绳子拉力F越大,绳子越容易断.故B错误.
C、D根据牛顿第二定律得:F=m
,m一定,丝速度大小相等时,绳短的容易断.故C正确,D错误.
故选AC
B、根据牛顿第二定律得:F=m
| 4π2r |
| T2 |
C、D根据牛顿第二定律得:F=m
| v2 |
| r |
故选AC
点评:本题考查灵活选择公式的能力,向心力的公式形式通常有下列几种,在不同条件下选用不同的形式:
Fn=m(2πn)2r=m
=m
=mω2r=mvω.
Fn=m(2πn)2r=m
| v2 |
| r |
| 4π2r |
| T2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
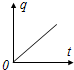 (2007?广州模拟)一个阻值为R的电阻两端加上电压U后,通过导体截面的电量q与通电时间t的图象如图所示,此图线的斜率(即tanα)等于( )
(2007?广州模拟)一个阻值为R的电阻两端加上电压U后,通过导体截面的电量q与通电时间t的图象如图所示,此图线的斜率(即tanα)等于( ) (2007?广州模拟)如图所示,有一混合正离子束先后通过正交电磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径R相同,则它们具有相同的( )
(2007?广州模拟)如图所示,有一混合正离子束先后通过正交电磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径R相同,则它们具有相同的( )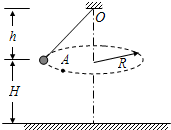 (2007?广州模拟)如图所示,用细线吊着一个小球,使小球在水平面内做半径为R的匀速圆周运动;圆周运动的水平面与悬点的距离为h,与水平地面的距离为H.若细线突在A处断裂,求小球在地面上的落点P与A的水平距离.
(2007?广州模拟)如图所示,用细线吊着一个小球,使小球在水平面内做半径为R的匀速圆周运动;圆周运动的水平面与悬点的距离为h,与水平地面的距离为H.若细线突在A处断裂,求小球在地面上的落点P与A的水平距离. (2007?广州模拟)如图所示表示作用在某物体上的合外力随时间变化的关系,若物体开始时是静止的,则前3s内( )
(2007?广州模拟)如图所示表示作用在某物体上的合外力随时间变化的关系,若物体开始时是静止的,则前3s内( )