题目内容
（12分）静止在水平面上的A、B两个物体通过一根拉直的轻绳相连，如图所示，轻绳长L=1m，承受的最大拉力为8N，A的质量m1=2kg，B的质量m2=8kg，A、B与水平面间的动摩擦因数μ=0.2，现用一逐渐增大的水平力F作用在B上，使A、B向右运动，当F增大到某一值时，轻绳刚好被拉断．(A、B可当做质点，g=10m/s2)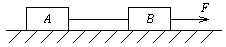
（1）求绳刚被拉断时F的大小；
（2）若绳刚被拉断时，A、B两物体的速度为2m/s，保持此时的F大小不变，则当A物体速度恰减至零时，A、B两物体间的距离为多少?
⑴40N（2）3.5m
解析试题分析：⑴对A、B整体，由牛顿第二定律，得：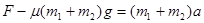
（2分）
隔离A物体，有：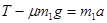
（2分）
当绳刚被拉断时，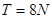
，联立上面两式，得：
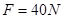（1分）
即绳刚被拉断时F的大小为40N
⑵绳拉断后，对A物体，有：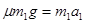
得：
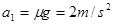（1分）
A物体历时t停下来，则：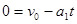
得：
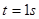（1分）
A物体在这段时间内前行的位移为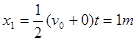
（1分）
对B物体，有：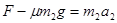 
得：
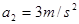（1分）
这段时间内B物体前行的位移为：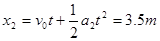
（1分）
则当A物体速度恰减至零时两者的距离为：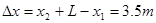
（2分）
即当A物体速度恰减至零时，A、B间的距离为3.5m
考点：考查牛顿第二定律的应用
点评：难度较小，求解第1问时注意绳子被拉断时为临界状态，此时两者的加速度依然相当，绳子的拉力增大到最大值
练习册系列答案
相关题目
静止在水平面上的A、B两个物体通过一根拉直的轻绳相连，如图，轻绳长L=1m，承受的最大拉力为8N，A的质量m1=2kg，B的质量m2=8kg，A、B与水平面间的动摩擦因数μ=0.2，现用一逐渐增大的水平力F作用在B上，使A、B向右运动，当F增大到某一值时，轻绳刚好被拉断（g=10m/s2）．
如图所示，质量为m=0.5kg的物体，静止在水平面上的A点．A点距光滑斜坡底端B点的距离为S=8m，物体运动时与水平面间的滑动摩擦系数μ=3/4．用恒力F作用在m上沿AB运动S'=5m后撤去F，m继续运动滑上斜坡后在C点水平飞出，正好垂直击中紧靠在斜坡右端、倾角为a=30°的斜面上．如果斜坡高度H=3m，求：
（2012?南海区模拟）如图所示，光滑水平面AB与粗糙斜面BC在B处通过圆弧衔接，质量M=0.3kg的小木块静止在水平面上的A点．现有一质量m=0.2kg子弹以v0=20m/s的初速度水平地射入木块（但未穿出），它们一起沿AB运动，并冲上BC．已知木块与斜面间的动摩擦因数μ=0.5，斜面倾角θ=45°，重力加速度g=10m/s2，木块在B 处无机械能损失．试求：
