题目内容
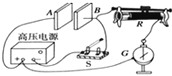
【题目】如图所示,AB为一段光滑水平轨道,BCD为一段光滑的圆弧轨道,半径为R。今有一质量为m、带电量为+q的绝缘小球,以速度v0从A点向B点运动,后又沿弧BC做圆周运动。小球到C点后由于速度较小,很难运动到最高点。如果当其运动至C点时,突然在轨道区域加一匀强电场和匀强磁场,使其能运动到最高点,此时轨道弹力为零,且贴着轨道做匀速圆周运动。求:

(1)所加磁场的方向和磁感应强度。
(2)小球从C点到D点过程中,电场力所做的功。
【答案】(1) (2)mgR
(2)mgR
【解析】试题分析:由动能定理可得小球运动至C点时的速度,当小球运动至C点时,在轨道区域加一匀强电场和匀强磁场,此时轨道弹力为零,且贴着轨道做匀速圆周运动,则重力与电场力平衡,则洛伦兹力提供向心力即可求得磁感应强度大小和方向;根据功的定义可求从C点到D点过程中,电场力做的功。
(1)小球到达C点的速度为vC,由动能定理得: ![]()
解得: ![]()
在C点同时加上匀强电场E和匀强磁场B后,要求小球做匀速圆周运动,对轨道的压力为零,必然是洛伦兹力提供向心力
由牛顿第二定律得: ![]()
解得: 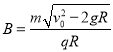
B的方向应垂直于纸面向外。
(2)要使小球做匀速圆周运动,必须加竖直向上匀强电场,且有:qE=mg
从C点到D点过程中,电场力做功为:W=qER=mgR 。

练习册系列答案
相关题目