Question

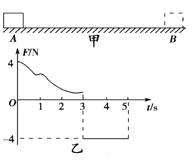
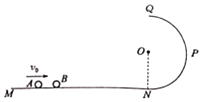
【题目】如图（a）所示，圆心为O的圆形区域，半径R＝10cm，MN为荧光屏，长度L＝100cm，P为屏的中点，圆形区域圆心O距离荧光屏s=20cm, OP垂直于MN，大量的带电粒子经U= 2000V电压加速，形成一连续的粒子束，沿半径方向进入圆形区域。当圆形区域内不加磁场时，带电粒子打在荧光屏中心P点，当圆形区域加一匀强磁场后，粒子束经磁场偏转打到荧光屏另一位置，通过改变磁场的大小、方向来改变粒子束打在荧光屏上的位置，磁感应强度B随时间t变化如图（b）所示，已知带电粒子的电量q＝1×10-3C，质量m＝1×10-8kg，不计粒子重力，忽略粒子在磁场中运动的时间，则下面说法正确的是（ ）

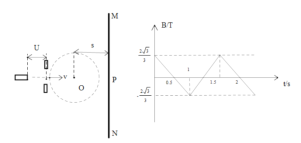
A. 粒子进入磁场区域的速度v＝2×103m／s

B. t＝0时刻进入磁场的粒子，速度偏转角度θ＝30°

C. 电子束打在荧光屏的范围宽度为40cm

D. 若B的最大值为2T，则t=0时刻进入磁场的粒子无法打到荧光屏上

Answer 1

【答案】CD

【解析】

根据Uq=mv2可得粒子进入磁场区域的速度：，选项A错误； t＝0时刻进入磁场的粒子， ，则运动半径；由几何关系可知，，α=300，则速度偏转角度θ＝2α=600，选项B错误；当t=0时刻射入的粒子射出磁场时打到屏上的位置距离P点最远，最远距离为，则粒子束打在荧光屏的范围宽度为2y=40cm，选项C正确；若B的最大值为2T，则粒子运动半径，则粒子出离磁场时速度方向平行光屏竖直向上，即t=0时刻进入磁场的粒子无法打到荧光屏上，选项D正确。故选CD.